-
试题检索 :
-
教材版本 :
-
课本 :
-
题型 :
-
难易度 :
某地区恩格尔系数y(%)与年份x的统计数据如下表:
| 年份x | 2004 | 2005 | 2006 | 2007 |
| 恩格尔系数y(%) | 47 | 45.5 | 43.5 | 41 |
从散点图可以看出y与x线性相关,且可得回归方程为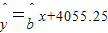 ,据此模型可预测2012年该地区的恩格尔系数(%)为 .
,据此模型可预测2012年该地区的恩格尔系数(%)为 .
通过圆与球的类比,由“半径为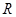 的圆的内接矩形中,以正方形的面积为最大,最大值为
的圆的内接矩形中,以正方形的面积为最大,最大值为 .”猜想关于球的相应命题为: .
.”猜想关于球的相应命题为: .
以下结论正确的是 .
(1)根据2×2列联表中的数据计算得出Χ2≥6.635,而P(Χ2≥6.635)≈0.01,则有99%的把握认为两个分类变量有关系
(2)在线性回归分析中,相关系数为r,|r|越接近于1,相关程度越大;|r|越小,相关程度越小
(3)在回归分析中,回归直线方程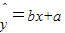 过点
过点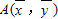
(4)在回归直线y=0.5x-85中,变量x=200时,变量y的值一定是15
观察:① ;
;
②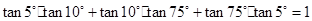 .
.
由此猜出一个一般式为 .
观察两相关量得如下数据: 求两变量间的回归直线方程 .
x
| -1
| -2
| -3
| -4
| -5
| 5
| 3
| 4
| 2
| 1
|
y
| -9
| -7
| -5
| -3
| -1
| 1
| 5
| 3
| 7
| 9
|
为了调查患慢性气管炎是否与吸烟有关,调查了339名50岁以上的人,调查结果如下表
| 患慢性气管炎
| 未患慢性气管炎
| 合计
|
吸烟
| 43
| 162
| 205
|
不吸烟
| 13
| 121
| 134
|
合计
| 56
| 283
| 339
|
根据列联表数据,求得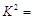 .
.
某人对一个地区人均工资x与该地区人均消费y进行统计调查得y与x具有相关关系,且回归直线方程为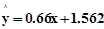 (单位:千元),若该地区人均消费水平为7.675,估计该地区人均消费额占人均工资收入的百分比约为______ _____.(精确到0.1%)
(单位:千元),若该地区人均消费水平为7.675,估计该地区人均消费额占人均工资收入的百分比约为______ _____.(精确到0.1%)
调查发现关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计数据. 由此资料所知y对x呈线性相关关系,回归直线方程为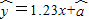 .设使用年限为10年,估计维修费用为 (万元)
.设使用年限为10年,估计维修费用为 (万元)
已知x,y之间的一组数据:y与x之间的线性性回归方程 =bx+a必过定点_ .
=bx+a必过定点_ .
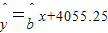 ,据此模型可预测2012年该地区的恩格尔系数(%)为 .
,据此模型可预测2012年该地区的恩格尔系数(%)为 . 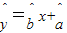 必经过点
必经过点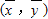 ;
; ;
;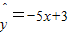 ,若变量x增加1个单位则y平均增加5个单位;
,若变量x增加1个单位则y平均增加5个单位;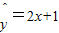 ,而实验得到的一组数据为(2,4.9),(3,7.1),(4,9.1),则残差平方和为0.03.
,而实验得到的一组数据为(2,4.9),(3,7.1),(4,9.1),则残差平方和为0.03.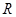 的圆的内接矩形中,以正方形的面积为最大,最大值为
的圆的内接矩形中,以正方形的面积为最大,最大值为 .”猜想关于球的相应命题为: .
.”猜想关于球的相应命题为: . 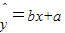 过点
过点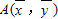
 ;
;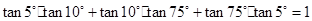 .
.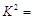 .
. 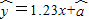 .设使用年限为10年,估计维修费用为 (万元)
.设使用年限为10年,估计维修费用为 (万元)  =bx+a必过定点_ .
=bx+a必过定点_ .