-
试题检索 :
-
教材版本 :
-
课本 :
-
题型 :
-
难易度 :
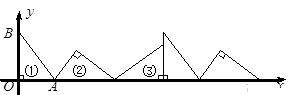
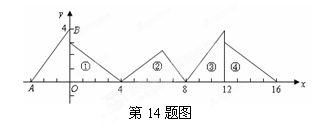
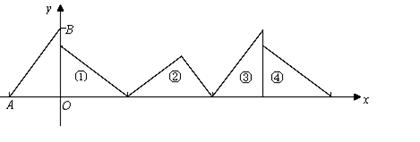
如图①,在△AOB中,∠AOB=90º,OA=3,OB=4.将△AOB沿x轴依次以
点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角
顶点的坐标为 .
已知,点A在变换T: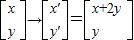 作用后,再绕原点逆时针旋转90°,得到点、B.若点B的坐标为(-3,4),求点A的坐标.
作用后,再绕原点逆时针旋转90°,得到点、B.若点B的坐标为(-3,4),求点A的坐标.
(1)选修4-2:矩阵与变换
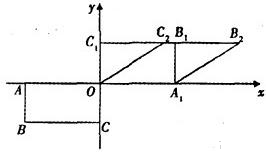
如图,矩形OABC的顶点O(0,0)、A(-2,0)、B(-2,-1)、C(0,-1).将矩形OABC绕坐标原点O旋转得到矩形OA1B1C1;再将矩形OA1B1C1沿x轴正方向作切变变换,得到平行四边形OA1B2C2,且点C2的坐标为(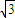 ,1).求将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.
,1).求将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.
已知△AOB的三顶点O(0,0),A(0,-4),B(2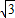 ,2),设△AOB在矩阵
,2),设△AOB在矩阵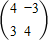 所对应的变换作用下得到△A′OB′,求∠OA′B′和△A′OB′的面积.
所对应的变换作用下得到△A′OB′,求∠OA′B′和△A′OB′的面积.
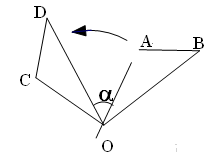

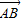 绕其起点沿逆时针方向旋转θ角,得到向量
绕其起点沿逆时针方向旋转θ角,得到向量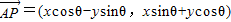 ,叫做把点B绕点A逆时针方向旋转θ角得到点P
,叫做把点B绕点A逆时针方向旋转θ角得到点P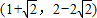 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转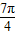 后得到点P,求点P的坐标
后得到点P,求点P的坐标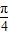 后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程. 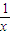 绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,
绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,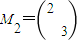 ,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.
,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.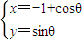 (θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.
(θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离. +
+ +
+ +L+
+L+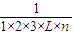 <2.
<2.
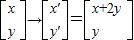 作用后,再绕原点逆时针旋转90°,得到点、B.若点B的坐标为(-3,4),求点A的坐标.
作用后,再绕原点逆时针旋转90°,得到点、B.若点B的坐标为(-3,4),求点A的坐标. 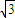 ,1).求将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.
,1).求将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵.
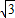 ,2),设△AOB在矩阵
,2),设△AOB在矩阵 所对应的变换作用下得到△A′OB′,求∠OA′B′和△A′OB′的面积.
所对应的变换作用下得到△A′OB′,求∠OA′B′和△A′OB′的面积.