首页 请复制到word或wps中编辑使用(ctrl+c,ctrl+v),vip用户页面底部可看到答案解析 公式上下对齐方法复制内容

正式的加减-化简求值

一.解答题 (共 18 小题)

1 . 已知，求代数式的值.

【答案解析】-10
先化，再代入求值即可.

考点：代数式求值

2 . 已知:，求

【答案解析】
由得：，所以，且
所以：
考点：完全平方公式

3 . 当x=2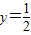，时，求代数式(x+y)(x-y)+(x-y)²-(x²-3xy)的值．

【答案解析】(x+y)(x-y)+(x-y)²-(x²-3xy)，
=x²-y²+x²-2xy+y²-x²+3xy，
=x²+xy，
当x=2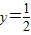，时，原式=2²+2×=5．
先利用平方差公式和完全平方公式把原式展开，再合并同类项，最后代数求值．

4 . 先化简下面的代数式，再求值：(x+2)(x-2)+2(x+1)，其中x=．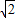

【答案解析】(x+2)(x-2)+2(x+1)，
=x²-4+2x+2，
=x²+2x-2，
当x=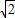时，
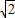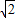原式=()²+2-2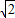=2+2-2=2．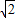
根据平方差公式和单项式乘多项式的法则去括号，合并同类项，将整式化为最简式，然后把x的值代入即可．

5 . 对于任何实数，我们规定符号的意义是：=ad-bc．按照这个规定请你计算：当x²-3x+1=0时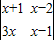，的值．

【答案解析】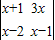=(x+1)(x-1)-3x(x-2)，
=x²-1-3x²+6x，
=-2x²+6x-1，
∵x²-3x+1=0，
∴x²-3x=-1，
∴原式=-2(x²-3x)-1=2-1=1．
应先根据所给的运算方式列式并根据平方差公式和单项式乘多项式的运算法则化简，再把已知条件整体代入求解即可．

6 . 先化简，再求值：(2a+1)²-2(2a+1)+3，其中a=．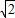

【答案解析】(2a+1)²-2(2a+1)+3，
=4a²+4a+1-4a-2+3，
=4a²+2，
当a=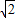时，
原式=4a²+2=4×(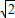)²+2=10．
根据完全平方公式和单项式乘多项式的法则去括号，合并同类项，将整式化为最简式，然后把a的值代入计算即可．

7 . 先化简下面的代数式，再求值：(x+1)²-2(x+2)，其中．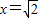

【答案解析】(x+1)²-2(x+2)，
=x²+2x+1-2x-4，
=x²-3，
当x=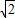时，原式=2-3=-1．
故答案为：-1．
运用完全平方公式和单项式与多项式的乘法，去括号，合并同类项，再求值．

8 . 化简并求值：[(a+b)²-(a+b)(a-b)]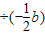，其中a=-2.008，b=-0.492．

【答案解析】原式=(a²+2ab+b²-a²+b²)，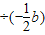
=(2ab+2b²)，
=-4a-4b．
当a=-2.008，b=-0.492时，
原式=-4(a+b)=-4×(-2.008-0.492)=-4×(-2.5)=10．
先把[(a+b)²-(a+b)(a-b)]展开合并同类项，再进行化简，最后把a、b的值代入求解即可．

9 . 已知x²-x=6，求代数式x(x+1)²-x²(x+1)-2x-8的值．

【答案解析】原式=x(x²+2x+1)-x³-x²-2x-8
=x³+2x²+x-x³-x²-2x-8
=x²-x-8
当x²-x=6时，原式=6-8=-2．
首先把多项式去括号，合并同类项后，整体代入求值．

10 . 已知a²+3a+1=0，求(2a+1)²-2(a²-a)+4的值．

【答案解析】(2a+1)²-2(a²-a)+4
=4a²+4a+1-2a²+2a+4
=2(a²+3a)+5．
∵a²+3a+1=0，
∴a²+3a=-1．
∴原式=2×(-1)+5=3．
将(2a+1)²-2(a²-a)+4转化为2(a²+3a)+5，把a²+3a=-1作为一个整体代入代数式求值．

11 . 先化简，再求值：(2x+3y)²-(2x+y)(2x-y)，其中x=，y=-．

【答案解析】原式=(4x²+12xy+9y²)-(4x²-y²)，
=4x²+12xy+9y²-4x²+y²，
=12xy+10y²，
当x=，y=-时，
原式=12×()×(-)+10×(-)²，
=-2+2.5
=．
先利用乘法公式化简代数式，再代入求值．

12 . 已知：x=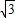+1，y=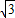-1，求下列各式的值．
(1)x²+2xy+y²；
(2)x²-y²．

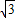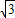【答案解析】(1)当x=+1，y=-1时，
原式=(x+y)²=(+1+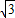-1)²=12；
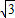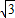(2)当x=+1，y=-1时，
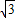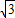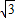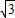原式=(x+y)(x-y)=(+1+-1)(+1-+1)=4．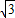
观察可知：(1)式是完全平方和公式，(2)是平方差公式．先转化，再代入计算即可．

13 . 先化简，再求值：(x+1)²-x(x-1)，其中x=．

【答案解析】(x+1)²-x(x-1)
=x²+2x+1-x²+x
=3x+1
把x=代入，原式=3×+1=2．
解题关键是化简，再代入求值．

14 . 先化简，再求值：
(1)x (x+2)-(x+1)(x-1)，其中x=-；
(2)已知x²-5x=14，求(x-1)(2x-1)-(x+1)²+1的值．

【答案解析】(1)x (x+2)-(x+1)(x-1)
=x²+2x-(x²-1)
=2x+1
把x=-代入上式得，
原式=2x+1=2×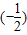+1=0；
(2)(x-1)(2x-1)-(x+1)²+1
=2x²-x-2x+1-(x²+2x+1)+1
=x²-5x+1，
∵x²-5x=14，
∴原式=x²-5x+1=14+1=15．
(1)先将整式去括号，然后再合并同类项，对整式进行化简，再把x=-代入求值；
(2)根据多项式乘法规则，对整式进行化简，然后再将x²-5x=14整体代入求值．

15 . 化简求值：[(x-y)²+y(4x-y)-8x]÷2x，其中x=8，y=2009．

【答案解析】[(x-y)²+y(4x-y)-8x]÷2x，
=(x²-2xy+y²+4xy-y²-8x)÷2x，
=(x²+2xy-8x)÷2x，
=x+y-4，
当x=8，y=2009时，
原式=×8+2009-4=2009．
本题应对方程去括号，合并同类项，将整式化为最简式，然后把x、y的值代入即可．

16 . 先化简，再求值：(-x²+5x+4)+(5x-4+2x²)，其中x=-2．

【答案解析】原式=(-x²+5x+4)+(5x-4+2x²)
=-x²+5x+4+5x-4+2x²=x²+10x
=x(x+10)．
∵x=-2，
∴原式=-16．
本题考查了整式的加减、去括号法则两个考点．先按照去括号法则去掉整式中的小括号，再合并整式中的同类项即可．

17 . 给出三个单项式：a²，b²，2ab．
(1)在上面三个单项式中任选两个相减，并进行因式分解；
(2)当a=2010，b=2009时，求代数式a²+b²-2ab的值．

【答案解析】(1)a²-b²=(a+b)(a-b)，
b²-a²=(b+a)(b-a)，
a²-2ab=a(a-2b)，
2ab-a²=a(2b-a)，
b²-2ab+b(b-2a)，
2ab-b²=b(2a-b)；
(写对任何一个式子给五分)

(2)a²+b²-2ab=(a-b)²，
当a=2010，b=2009时，原式=(a-b)²=(2010-2009)²=1．
本题要灵活运用整式的加减运算、平方差公式和完全平方公式．

18 . 先化简，再求值：(x+1)²-(x-1)(2x-1)+5，其中x²-5x=5．

【答案解析】(x+1)²-(x-1)(2x-1)+5，
=(x²+2x+1)-(2x²-x-2x+1)+5，
=-x²+5x+5；
当x²-5x=5时，
原式=-x²+5x+5=-5+5=0．
根据完全平方公式和多项式的乘法计算，再合并同类项，然后将x²-5x=5整体代入求值．