首页 请复制到word或wps中编辑使用(ctrl+c,ctrl+v),vip用户页面底部可看到答案解析 公式上下对齐方法
2025学年浙江省衢州市五校联盟预测卷
一.填空题
(共 50 小题)
1 . 若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=|x|,函数y=g(x)是偶函数,且x∈(0,+∞)时,g(x)=|log3x|.则函数y=f(x)图象与函y=g(x)图象的交点个数为______
【答案解析】∵函数y=f(x)(x∈R)满足f(x+2)=f(x),
∴它是周期函数,周期是2,
∵函数y=g(x)是偶函数
∴它的图象关于y轴对称.
画图:
由图知,共6个交点.
故填:6.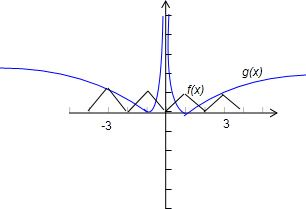
2 .
已知函数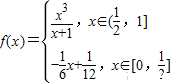 ,函数
,函数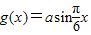 -a+1(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
-a+1(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
【答案解析】由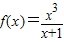 ,得:
,得: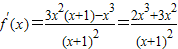 ,
,
当x∈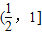 时,f′(x)>0,所以函数f(x)在
时,f′(x)>0,所以函数f(x)在 上为增函数,所以f(x)∈
上为增函数,所以f(x)∈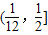 ,
,
当x∈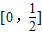 时,函数f(x)为减函数,f(x)∈
时,函数f(x)为减函数,f(x)∈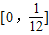 ,所以在[0,1]上f(x)∈
,所以在[0,1]上f(x)∈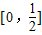 ,
,
函数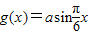 -a+1,当x∈[0,1]时,
-a+1,当x∈[0,1]时,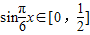 ,
,
所以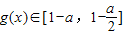
若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,说明函数函数g(x)的最大值与最小值中至少一个在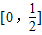 中,
中,
所以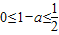 或
或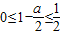 ,解得:
,解得: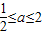 ,
,
所以实数a的取值范围是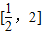 .
.
故答案为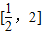 .
.
根据给出的函数f(x)的解析式求出其值域为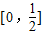 ,然后求出函数g(x)在x∈[0,1]上的值域,由存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,说明函数g(x)的最值中至少一个在
,然后求出函数g(x)在x∈[0,1]上的值域,由存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,说明函数g(x)的最值中至少一个在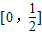 范围内,最后列式求解a的范围.
范围内,最后列式求解a的范围.
3 .
对于幂函数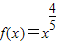 ,若0<x1<x2,则
,若0<x1<x2,则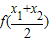 ,
,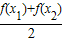 大小关系是 .
大小关系是 .
【答案解析】由于幂函数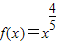 在(0,+∞)上是增函数,图象是上凸的,则当0<x1<x2 时,应有
在(0,+∞)上是增函数,图象是上凸的,则当0<x1<x2 时,应有 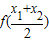 >
>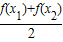 ,
,
故答案为 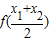 >
>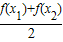 .
.
根据幂函数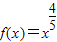 在(0,+∞)上是增函数,图象是上凸的,则当0<x1<x2 时,应有
在(0,+∞)上是增函数,图象是上凸的,则当0<x1<x2 时,应有 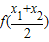 >
>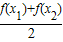 ,由此可得结论.
,由此可得结论.
4 .
已知幂函数f(x)=xa的图象过点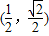 ,则f(x)在(0,+∞)单调递 .
,则f(x)在(0,+∞)单调递 .
【答案解析】∵幂函数f(x)=xa的图象过点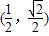 ,
,
∴ a=
a=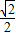
解得a=
∵a>0
∴f(x)在(0,+∞)单调递增
故答案为:增
根据已知幂函数f(x)=xa的图象过点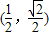 求出函数的解析式,进而根据幂函数的单调性,得到答案.
求出函数的解析式,进而根据幂函数的单调性,得到答案.
5 .
以下是关于函数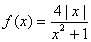 的四个命题:
的四个命题:
①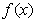 的图像关于
的图像关于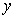 轴对称;
轴对称;
②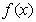 在区间
在区间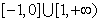 上单调递减;
上单调递减;
③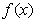 在
在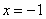 处取得极小值,在
处取得极小值,在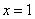 处取得极大值;
处取得极大值;
④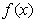 的有最大值,无最小值;
的有最大值,无最小值;
⑤若方程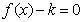 至少有三个不同的实根,则实数
至少有三个不同的实根,则实数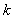 的取值范围是
的取值范围是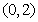 。
。
其中为真命题的是____ (请填写你认为是真命题的序号).
【答案解析】①⑤
6 .
已知直线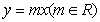 与函数
与函数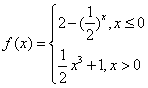 的图象恰有三个不同的公共点,则实数m的取值范围是 .
的图象恰有三个不同的公共点,则实数m的取值范围是 .
【答案解析】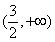
7 .
一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长、宽分别为x,y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是______(填序号). 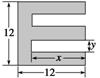
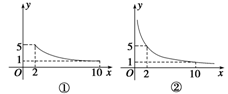
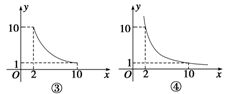
【答案解析】①
8 .
已知函数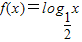 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称,
(1)若g(a)g(b)=2,且a<0,b<0,则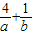 的最大值为
的最大值为
(2)设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2-x)=f(x+2),且当x∈[-2,0]时,f(x)=g(x)-1,若关于x的方程f(x)-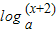 =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
【答案解析】(1)根据题意,g(x)=( )x=2-x,
)x=2-x,
若g(a)g(b)=2,则有2-(a+b)=2,即a+b=-1,
则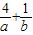 =-[(-a)+(-b)][
=-[(-a)+(-b)][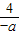 +
+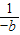 ]=-[5+
]=-[5+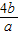 +
+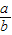 ],
],
又由a<0,b<0,则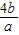 >0且
>0且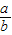 >0,故
>0,故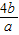 +
+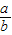 ≥4,
≥4,
则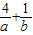 =-[5+
=-[5+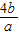 +
+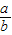 ]≤-9,
]≤-9,
即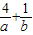 的最大值为-9;
的最大值为-9;
(2)对于任意的x∈R,都有f(x-2)=f(2+x),∴函数f(x)是一个周期函数,且T=4.
又∵当x∈[-2,0]时,f(x)=( )x-1,且函数f(x)是定义在R上的偶函数,
)x-1,且函数f(x)是定义在R上的偶函数,
若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,
则函数y=f(x)与y=-loga(x+2)在区间(-2,6]上有三个不同的交点,
又f(-2)=f(2)=3,分析可得有 loga4<3,且loga8>3,解得: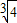 <a<2,
<a<2,
则a的取值范围是(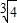 ,2)
,2)
故答案为(1):-9;(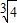 ,2).
,2).
(1)根据题意,由反函数的定义以及对数函数、指数函数的性质可得g(x)=( )x=2-x,进而结合题意可得2-(a+b)=2,即a+b=-1,对
)x=2-x,进而结合题意可得2-(a+b)=2,即a+b=-1,对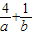 变形可得其等于-[5+
变形可得其等于-[5+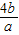 +
+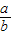 ],由基本不等式的性质可得
],由基本不等式的性质可得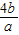 +
+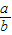 ≥4,代入
≥4,代入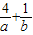 =-[5+
=-[5+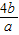 +
+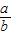 ]可得其最大值,即可得答案.
]可得其最大值,即可得答案.
(2)根据题意,分析可得函数f(x)是一个周期函数,且周期为4,将方程f(x)-logax+2=0恰有3个不同的实数解,转化为函数f(x)的与函数y=-logax+2的图象恰有3个不同的交点,数形结合即可得到实数a的取值范围.
9 .
函数![]() 的图象为
的图象为![]() ,如下结论中正确的是__________(写出所有正确结论的编号). ①图象
,如下结论中正确的是__________(写出所有正确结论的编号). ①图象![]() 关于直线
关于直线![]() 对称;
对称;
②图象![]() 关于点
关于点![]() 对称;③函数
对称;③函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象
个单位长度可以得到图象![]() .
.
【答案解析】①②③
10 .
设函数 ,给出下列四个命题:
,给出下列四个命题:
①函数f(|x|)为偶函数;
②若|f(a)|=|f(b)|其中a>0,b>0,a≠b,则ab=1;
③函数f(-x2+2x)在(1,+∞)上为单调增函数;
④若0<a<1,则|f(1+a)|<|f(1-a)|;
则正确命题的序号是 .
【答案解析】∵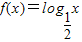
∴①函数f(|x|)为偶函数,此命题正确,因为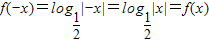 此函数是一个偶函数,命题是正确命题;
此函数是一个偶函数,命题是正确命题;
②若|f(a)|=|f(b)|其中a>0,b>0,a≠b,则ab=1,此命题是正确命题,因为|f(a)|=|f(b)|其中a>0,b>0,a≠b,故有f(a)+f(b)=0,即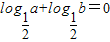 ,故有ab=1;
,故有ab=1;
③函数f(-x2+2x)的定义域是(0,2),故复合函数f(-x2+2x)在(1,+∞)上为单调增函数错;
④若0<a<1,则|f(1+a)|<|f(1-a)|,此命题,因为由题意f(1+a)<0,f(1-a)>0,若有|f(1+a)|<|f(1-a)|成立,则f(1+a)+f(1-a)>0,即f(1-a2)>0,即1-a2∈(0,1)显然成立;
综上①②④都是正确命题
故答案为①②④
由题设条件函数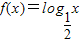 ,根据对数的函数的性质对四个命题进行判断,得出正误
,根据对数的函数的性质对四个命题进行判断,得出正误
①函数f(|x|)为偶函数,由偶函数的定义进行判断正误;
②若|f(a)|=|f(b)|其中a>0,b>0,a≠b,则ab=1,由对数的性质进行推断即可判断此命题的正误;
③函数f(-x2+2x)在(1,+∞)上为单调增函数,由复合函数的单调性易判断;
④若0<a<1,则|f(1+a)|<|f(1-a)|,对两个数作差比较出它们的大小,得出正误;
11 . 将函数f1(x)=3x的图象向右平移2个单位后得到f2(x)的图象,再作与f2(x)关于y轴对称的f3(x)的图象,则f3(x)的函数解析式为f3(x)= .
【答案解析】∵将函数f1(x)=3x的图象水平向右平移2个单位后得到:
f2(x)=3x-2
再关于y轴对称,将原函数式中的y不变,x换成-x,得到函数:y=3-x-2
即:f3(x)=3-x-2
故答案为:3-x-2
先写出将函数f1(x)=3x的图象水平向右平移2个单位后得到f2(x)的解析式,再根据:“关于y轴对称”写出f3(x)的函数解析式即可.
12 .
定义:对于一个函数f(x)(x∈D),若存在两条距离为d的直线y=kx+m1和y=kx+m2,使得在x∈D时,kx+m1≤f(x)≤kx+m2恒成立,则称函数f(x)在D内有一个宽度为d的通道.下列函数:①f(x)=e-x,②f(x)=sinx,③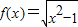 ,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是 .
,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是 .
【答案解析】对于①,当x∈[1,+∞)时, ,故在[1,+∞)有一个宽度为1的通道,两条直线可取y=0,y=1;
,故在[1,+∞)有一个宽度为1的通道,两条直线可取y=0,y=1;
对于②,当x∈[1,+∞)时,-1≤sinx≤1,故在[1,+∞)不存在一个宽度为1的通道;
对于③,当x∈[1,+∞)时, ,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为
,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为 ,满足在[1,+∞)有一个宽度为1的通道;
,满足在[1,+∞)有一个宽度为1的通道;
对于④,当x∈[1,+∞)时,f(x)∈[1,+∞),故在[1,+∞)不存在一个宽度为1的通道;
故答案为:①③
对于①,当x∈[1,+∞)时,确定函数的值域,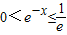 ,故可知两条直线可取y=0,y=1;对于②,当x∈[1,+∞)时,-1≤sinx≤1;对于③,当x∈[1,+∞)时,
,故可知两条直线可取y=0,y=1;对于②,当x∈[1,+∞)时,-1≤sinx≤1;对于③,当x∈[1,+∞)时, ,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为
,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为 ,满足在[1,+∞)有一个宽度为1的通道;
,满足在[1,+∞)有一个宽度为1的通道;
对于④,当x∈[1,+∞)时,f(x)∈[1,+∞),故可得结论.
13 .
我们把具有以下性质的函数f(x)称为“好函数”:对于在f(x)定义域内的任意三个数a,b,c,若这三个数能作为三角形的三边长,则f(a),f(b),f(c)也能作为三角形的三边长.现有如下一些函数:
①
②
③f(x)=ex,x∈(0,1)
④f(x)=sinx,x∈(0,π).
其中是“好函数”的序号有 .
【答案解析】任给三角形,设它的三边长分别为a,b,c,不妨设c是最大边,且a+b>c
① ,∵
,∵ ,∴函数f(x)是“好函数”;
,∴函数f(x)是“好函数”;
②f(x)=1-x,∵f(a)+f(b)-f(c)=1+c-(a+b),a,b,c∈(0, ),∴f(a)+f(b)-f(c)>0,∴f(a)+f(b)>f(c),∴函数f(x)是“好函数”;
),∴f(a)+f(b)-f(c)>0,∴f(a)+f(b)>f(c),∴函数f(x)是“好函数”;
③f(x)=ex, ,若
,若 ,即ec<4,∵c∈(0,1),∴结论成立,∴函数f(x)是“好函数”;
,即ec<4,∵c∈(0,1),∴结论成立,∴函数f(x)是“好函数”;
④f(x)=sinx,若f(a)+f(b)=sina+sinb=2sin cos
cos >sinc,则∵x∈(0,π),-π<a-b<c,∴结论不一定成立,∴函数f(x)不是“好函数”;
>sinc,则∵x∈(0,π),-π<a-b<c,∴结论不一定成立,∴函数f(x)不是“好函数”;
故答案为:①②③
任给三角形,设它的三边长分别为a,b,c,则a+b>c,
① ,可得函数f(x)是“好函数”;
,可得函数f(x)是“好函数”;
②作差,验证f(a)+f(b)>f(c),可得函数f(x)是“好函数”;
③ ,若
,若 ,即ec<4,由c∈(0,1),可得结论成立;
,即ec<4,由c∈(0,1),可得结论成立;
④若f(a)+f(b)=sina+sinb=2sin cos
cos >sinc,结论不一定成立.
>sinc,结论不一定成立.
14 .
已知函数f(x)= ,a∈R.若对于任意的x∈N,f (x)≥4恒成立,则a的取值范围是 .
,a∈R.若对于任意的x∈N,f (x)≥4恒成立,则a的取值范围是 .
【答案解析】∵函数f (x)= ,且f (x)≥4,对于任意的x∈N*恒成立
,且f (x)≥4,对于任意的x∈N*恒成立
即a≥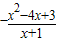 =
= =
=
令g(x)= ,则g(x)≤6-4
,则g(x)≤6-4 ,当且仅当x=2
,当且仅当x=2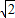 -1时g(x)取最大值
-1时g(x)取最大值
又∵x∈N*,
∴当x=2时,g(x)取最大值
故a≥
即a的取值范围是[ ,+∞)
,+∞)
故答案为:[ ,+∞)
,+∞)
根据已知中函数f (x)= ,a∈R.若对于任意的x∈N*,f (x)≥4恒成立,我们可将其转化为a≥
,a∈R.若对于任意的x∈N*,f (x)≥4恒成立,我们可将其转化为a≥ 恒成立,进而将其转化为a≥g(x)max=
恒成立,进而将其转化为a≥g(x)max= ,解不等式可得a的取值范围.
,解不等式可得a的取值范围.
15 .
设函数f(x)的定义域为D,令M={k|f(x)≤k恒成立,x∈D},N={k|f(x)≥k恒成立,x∈D},已知 ,其中x∈[0,2],若4∈M,2∈N,则a的范围是 .
,其中x∈[0,2],若4∈M,2∈N,则a的范围是 .
【答案解析】由题意,x∈[0,2]时, ,∴
,∴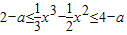
令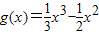 ,则g′(x)=x2-x=x(x-1)
,则g′(x)=x2-x=x(x-1)
∵x∈[0,2],∴函数在[0,1]上单调递减,在[1,2]上单调递增
∴x=1时,g(x)min=-
∵g(0)=0,g(2)=
∴g(x)max=
∴2-a≤- 且4-a≥
且4-a≥
∴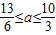
故答案为: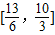
由题意,x∈[0,2]时, ,确定
,确定 的最值,即可求得a的范围.
的最值,即可求得a的范围.
16 .
定义一:对于一个函数f(x)(x∈D),若存在两条距离为d的直线y=kx+m1和y=kx+m2,使得在x∈D时,kx+m1≤f(x)≤kx+m2 恒成立,则称函数f(x)在D内有一个宽度为d的通道.
定义二:若一个函数f(x),对于任意给定的正数ɛ,都存在一个实数x,使得函数f(x)在[x,+∞)内有一个宽度为ɛ的通道,则称f(x)在正无穷处有永恒通道.下列函数:
①f(x)=lnx,②f(x)= ,③f(x)=
,③f(x)=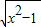 ,④f(x)=x2,⑤f(x)=e-x,
,④f(x)=x2,⑤f(x)=e-x,
其中在正无穷处有永恒通道的函数的序号是 .
【答案解析】①f(x)=lnx,随着x的增大,函数值也在增大,无渐近线,故不存在一个实数x,使得函数f(x)在[x,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处无永恒通道;
②f(x)=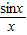 ,随着x的增大,函数值趋近于0,对于任意给定的正数ɛ,都存在一个实数x,使得函数f(x)在[x,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道;
,随着x的增大,函数值趋近于0,对于任意给定的正数ɛ,都存在一个实数x,使得函数f(x)在[x,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道;
③f(x)=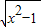 ,随着x的增大,函数值也在增大,有两条渐近线y=±x,对于任意给定的正数ɛ,都存在一个实数x,使得函数f(x)在[x,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道;
,随着x的增大,函数值也在增大,有两条渐近线y=±x,对于任意给定的正数ɛ,都存在一个实数x,使得函数f(x)在[x,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道;
④f(x)=x2,随着x的增大,函数值也在增大,无渐近线,故不存在一个实数x,使得函数f(x)在[x,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处无永恒通道;
⑤f(x)=e-x,随着x的增大,函数值趋近于0,趋近于x轴,对于任意给定的正数ɛ,都存在一个实数x,使得函数f(x)在[x,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道.
故答案为:②③⑤
根据定义一与定义二,对所给函数进行逐一进行判定,解题的关键看函数的单调性和是否有渐近线等.
17 .
已知函数①f(x)=3lnx;②f(x)=3ecosx;③f(x)=3ex;④f(x)=3cosx.其中对于f(x)定义域内的任意一个自变量x1都存在唯一个个自变量x2,使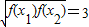 成立的函数序号是 .
成立的函数序号是 .
【答案解析】根据题意可知:
①f(x)=3lnx,x=1时,lnx没有倒数,不成立;
②f(x)=3ecosx,任一自变量f(x)有倒数,但所取x】的值不唯一,不成立;
③f(x)=3ex,任意一个自变量,函数都有倒数,成立;
④f(x)=3cosx,当x=2kπ+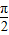 时,函数没有倒数,不成立.
时,函数没有倒数,不成立.
所以成立的函数序号为③
故答案为③
根据题意可知其中对于f(x)定义域内的任意一个自变量x1都存在唯一个个自变量x2,使 即要判断对于任意一个自变量x,函数都有倒数,所以判断函数恒有倒数即
即要判断对于任意一个自变量x,函数都有倒数,所以判断函数恒有倒数即 成立.
成立.
18 .
.
①极坐标系中,极点到直线ρcosθ+ρsinθ=2的距离等于 .
②不等式|x+3|-|x-1|≤a2-3a对任意实数x恒成立,则实数a的取值范围为 .
【答案解析】①直线ρcosθ+ρsinθ=2的极坐标方程为:
x+y-2=0,
∴极点到直线ρcosθ+ρsinθ=2的距离等于: .
.
故答案为:
②令y=|x+3|-|x-1|
当x>1时,y=x+3-x+1=4
当x<-3时,y=-x-3+x-1=-4
当-3≤x≤1时,y=x+3+x-1=2x+2 所以-4≤y≤4
所以要使得不等式|x+3|-|x-1|≤a2-3a对任意实数x恒成立
只要a2-3a≥4即可
∴a≤-1或a≥4
故答案为:(-∞,-1]∪[4,+∞)
①先利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换将直线ρcosθ+ρsinθ=2的化成直角坐标方程,再在直角坐标系中算出极点到直线的距离即可.
②先去绝对值符号确定|x+3|-|x-1|的取值范围,然后让a2-3a大于它的最大值即可.
19 .
若函数f(x)满足∃m∈R,m≠0,对定义域内的任意x,f(x+m)=f(x)+f(m)恒成立,则称f(x)为m函数,现给出下列函数:
①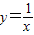 ; ②y=2x;③y=sinx;④y=1nx
; ②y=2x;③y=sinx;④y=1nx
其中为m函数的序号是 .(把你认为所有正确的序号都填上)
【答案解析】①若 ,则由f(x+m)=f(x)+f(m)得
,则由f(x+m)=f(x)+f(m)得 ,即
,即 ,
,
所以不存在常数m使f(x+m)=f(x)+f(m)成立,所以①不是m函数.
②若f(x)=2x,由f(x+m)=f(x)+f(m)得,2(x+m)=2x+2m,此时恒成立,所以②y=2x是m函数.
③若f(x)=sinx,由f(x+m)=f(x)+f(m)得sin(x+m)=sinx+sinm,所以当m=π时,f(x+m)=f(x)+f(m)成立,所以③y=sinx是m函数.
④若f(x)=1nx,则由f(x+m)=f(x)+f(m)得ln(x+m)=lnx+lnm,即ln(x+m)=lnmx,所以x+m=mx,要使x+m=mx成立则有 ,所以方程无解,所以④y=1nx不是m函数.所以为m函数的序号是②③.
,所以方程无解,所以④y=1nx不是m函数.所以为m函数的序号是②③.
故答案为:②③
根据m函数定义逐项判断即可.
20 . 若f(x)是定义在R上的函数,满足对任意的x,y∈R,都有f(x+y)=f(x)f(y)成立,且f(2)=3,则f(8)= .
【答案解析】由题意可知:对任意的x,y∈R,都有f(x+y)=f(x)f(y)成立,
所以x=y=2,可知f(4)=f(2+2)=f(2)•f(2),所以f(4)=9;
令x=y=4,可知f(8)=f(4+4)=f(4)•f(4)=92=81.
故答案为:81.
本题考查的是抽象函数及其应用问题.在解答时,可充分利用条件:对任意的x,y∈R,都有f(x+y)=f(x)f(y)成立,中的任意性,对x、y取特值进行计算即可.
21 . 已知函数y=f(n),满足f(1)=2,且f(n+1)=3f(n),n∈N+,则 f(3)的值为 .
【答案解析】∵f(1)=2,且f(n+1)=3f(n),n∈N+,
∴f(2)=3f(1)=6,
f(3)=f(2+1)=3f(2)=18,
故答案为 18.
由f(1)=2,且f(n+1)=3f(n),n∈N+,先求出f(2),再利用f(3)=f(2+1)=3f(2)可求 f(3)的值.
22 . y=f(x)有反函数y=f-1(x),又y=f(x+2)与y=f-1(x-1)互为反函数,则f-1(2007)-f-1(1)= .
【答案解析】y=f(x+2)
x+2=f-1(y)
∴x=f-1(y)-2
因此y=f(x+2)的反函数为y=f-1(x)-2
因此f-1(x-1)=f-1(x)-2
f-1(x)=f-1(x-1)+2对所有x恒成立
f-1(2007)-f-1(1)=2×(2007-1)=4012
故答案为:4012
求出y=f(x+2)的反函数,根据已知列出方程得到f-1(x)=f-1(x-1)+2,通过迭代求出f-1(2009)-f-1(1)的值.
23 .
函数f(x)的定义域为D,若对任意的x1、x2∈D,当x1<x2时,都有f(x1)≤f(x2),则称函数f(x)在D上为“非减函数”.设函数g(x)在[0,1]上为“非减函数”,且满足以下三个条件:
(1)g(0)=0;
(2)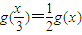 ;
;
(3)g(1-x)=1-g(x),
则g(1)= 、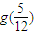 = .
= .
【答案解析】①在(3)中令x=0得g(1)=1-g(0)=1,∴g(1)=1;
②在(2)中令x=1得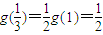 ,在(3)中令
,在(3)中令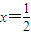 得
得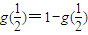 ,故
,故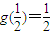 ,
,
∵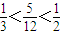 ,∴
,∴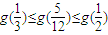 ,故
,故 .
.
故答案分别为1, .
.
①在(3)中令x=0即可得出g(1);②在(2)中令x=1得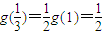 ,在(3)中令
,在(3)中令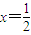 得
得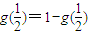 ,再利用函数g(x)在[0,1]上为“非减函数”即可得出.
,再利用函数g(x)在[0,1]上为“非减函数”即可得出.
24 .
给出下列四个命题:
①已知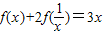 ,则函数g(x)=f(2x)在(0,1)上有唯一零点;
,则函数g(x)=f(2x)在(0,1)上有唯一零点;
②对于函数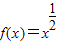 的定义域中任意的x1、x2(x1≠x2)必有
的定义域中任意的x1、x2(x1≠x2)必有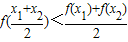 ;
;
③已知f(x)=|2-x+1-1|,a<b,f(a)<f(b),则必有0<f(b)<1;
④已知f(x)、g(x)是定义在R上的两个函数,对任意x、y∈R满足关系式f(x+y)+f(x-y)=2f(x)•g(y),且f(0)=0,但x≠0时f(x)•g(x)≠0.则函数f(x)、g(x)都是奇函数.
其中正确命题的序号是 .
【答案解析】∵f(x)+2f(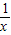 )=3x①,
)=3x①,
∴2f(x)+f( )=
)=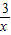 ②,
②,
②×2-①得:f(x)=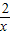 -x,
-x,
∴g(x)=f(2x)=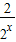 -2x=
-2x=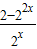 ,由g(x)=0解得x=
,由g(x)=0解得x= ,
,
∴函数g(x)=f(2x)在(0,1)上有唯一零点;①正确;
②对于函数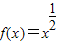 的定义域中任意的x1、x2(x1≠x2)必有
的定义域中任意的x1、x2(x1≠x2)必有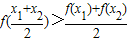 ,故②错误;
,故②错误;
对于③f(x)=|2-x+1-1|,
∵a<b,f(a)<f(b),
∴f(x)=|2-x+1-1|在(a,b)上单调递增,
∴f(x)=1-2-x+1(2-x+1-1<0即x>1),
∴b>1,
∴0<f(b)=|2-b+1-1|=1-2-b+1<1,故③正确;
对于④,令x=0,有f(-y)+f(y)=0,f(-y)=-f(y)函数f(x)是奇函数,
∵x≠0时,f(x)•g(x)≠0,
∴g(-y)=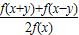 =g(y),
=g(y),
∴函数g(x)是偶函数,
∵④错误.
综上所述,①③正确.
故答案为:①③.
①通过方程组求得f(x),从而求得g(x),由g(x)=0即可判断其正误;
②可借助图形判断其正误;
③可利用f(x)=|2-x+1-1|在(a,b)上单调递增,判断③;
④分别判断f(x),g(x)的奇偶性,即可判断④的正误.
25 .
若f(x)满足:
(1)定义域为R;
(2)f(x1+x2)=f(x1)f(x2);
(3)f(1)=3;
(4)对任意x1<x2,f(x1)<f(x2).
则函数f(x)的一个解析式为 .
【答案解析】根据题意,可取指数函数f(x)=3x
f(x)满足:
(1)定义域为R;
(2)f(x1+x2)=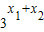 =
=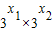 =f(x1)f(x2);
=f(x1)f(x2);
(3)f(1)=31=3;
(4)对任意x1<x2,f(x1)<f(x2),即函数为增函数.
故答案为:f(x)=3x
可取指数函数f(x)=3x,再验证满足所给的四个性质即可.
26 .
如果函数f(x)满足:对任意实数a,b都有f(a+b)=f(a)f(b),且f(1)=1,则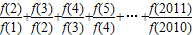 = .
= .
【答案解析】因为f(a+b)=f(a)f(b),且f(1)=1,
所以f(a+1)=f(a)f(1)=f(a),
故有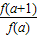 =1.
=1.
∴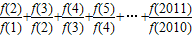 =1+1+1+…+1=2010.
=1+1+1+…+1=2010.
故答案为:2010.
先有f(a+b)=f(a)f(b),且f(1)=1,得到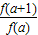 =1,再把所求结论代入即可求出结果.
=1,再把所求结论代入即可求出结果.
27 .
设函数y=f(x)在(a,b)上的导函数为f'(x),f'(x)在(a,b)上的导函数为f''(x),若在(a,b)上,f''(x)<0恒成立,则称函数f(x)在(a,b)上为“凸函数”.已知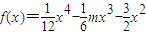 .
.
(Ⅰ)若f(x)为区间(-1,3)上的“凸函数”,则实数m=
(Ⅱ)若当实数m满足|m|≤2时,函数f(x)在(a,b)上总为“凸函数”,则b-a的最大值为 .
【答案解析】由函数 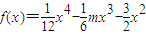 得,f″(x)=x2-mx-3(3分)
得,f″(x)=x2-mx-3(3分)
(Ⅰ)若f(x)为区间(-1,3)上的“凸函数”,则有f″(x)=x2-mx-3<0在区间(-1,3)上恒成立,
由二次函数的图象,当且仅当 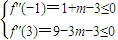 ,
,
即 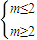 ⇔m=2.(7分)
⇔m=2.(7分)
(Ⅱ)当|m|≤2时,f″(x)=x2-mx-3<0恒成立⇔当|m|≤2时,mx>x2-3恒成立.(8分)
当x=0时,f″(x)=-3<0显然成立.(9分)
当x>0,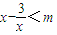
∵m的最小值是-2.
∴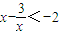 .
.
从而解得0<x<1(11分)
当x<0,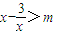
∵m的最大值是2,∴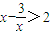 ,
,
从而解得-1<x<0.(13分)
综上可得-1<x<1,从而(b-a)max=1-(-1)=2(14分)
故答案为:2;2.
(Ⅰ)函数在区间(-1,3)上为“凸函数”,所以f″(x)<0,即对函数y=f(x)二次求导,转化为不等式问题解决即可;
(Ⅱ)利用函数总为“凸函数”,即f″(x)<0恒成立,转化为不等式恒成立问题,讨论解不等式即可.
28 .
函数f(x)对任意正整数a,b满足条件f(a+b)=f(a)•f(b)且f(1)=2,则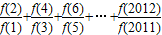 = .
= .
【答案解析】在f(a+b)=f(a)•f(b)中,令b=1可得,f(a+1)=f(a)•f(1),即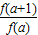 =f(1),
=f(1),
又由f(1)=2,则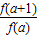 =2,
=2,
即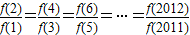 =2,
=2, =2+2+…+2=2×1006=2012;
=2+2+…+2=2×1006=2012;
故答案为:2012.
根据题意,在f(a+b)=f(a)•f(b)中,令b=1可得,f(a+1)=f(a)•f(1),可以变形为 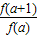 =f(1)=2,代入
=f(1)=2,代入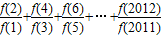 中可得答案.
中可得答案.
29 .
设定义在R上的函数f(x)同时满足以下三个条件:①f(x)+f(-x)=0;②f(x+2)=f(x);③当0<x<1时,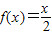 ,则
,则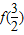 = .
= .
【答案解析】∵f(x)+f(-x)=0,
∴f(x)是奇函数,
∵f(x+2)=f(x),
∴f(x)的周期为2,
∴f( )=-f(-
)=-f(- )=-f(-
)=-f(- +2)=-f(
+2)=-f( ),
),
∴当x= 时,
时,
f( )=
)= ,
,
∴f( )=-
)=- ,
,
故答案为- .
.
首先判断出函数是奇函数,然后根据f(x+2)=f(x)判断出函数的周期为2,故可知f( )=-f(-
)=-f(- )=-f(-
)=-f(- +2)=-f(
+2)=-f( ),进而可得答案.
),进而可得答案.
30 .
若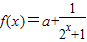 是奇函数,则a= .
是奇函数,则a= .
【答案解析】函数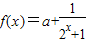 的定义域为R,且为奇函数,
的定义域为R,且为奇函数,
则 f(0)=a+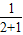 =0,得a+
=0,得a+ =0,得 a=-
=0,得 a=- ,
,
检验:若a=- ,则f(x)=
,则f(x)=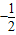 +
+ =
=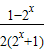 ,
,
又f(-x)=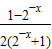 =-
=-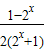 =-f(x) 为奇函数,符合题意.
=-f(x) 为奇函数,符合题意.
故答案为- .
.
充分不必要条件:若奇函数定义域为R(即x=0有意义),则f(0)=0.或用定义:f(-x)=f(x)直接求a.
31 .
若f(x)是奇函数,g(x)是偶函数,且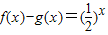 ,则f(1)g(0)g(-2)从小到大的顺序为 .
,则f(1)g(0)g(-2)从小到大的顺序为 .
【答案解析】∵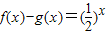 ,①
,①
又∵f(x)是奇函数,g(x)是偶函数
∴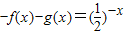 ②
②
由①②解得: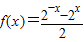 ,
,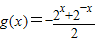
∴f(1)=- ,g(0)=-1,g(-2)=
,g(0)=-1,g(-2)=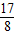
∴g(0)<f(1)<g(-2)
故答案为:g(0)<f(1)<g(-2)
先通过f(x),g(x)的奇偶性来产生另一个方程,再与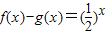 组成方程组求解函数的解析式,再通过函数值比较.
组成方程组求解函数的解析式,再通过函数值比较.
32 .
函数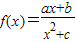 的图象如下,则a,b,c的大小顺序为 .
的图象如下,则a,b,c的大小顺序为 .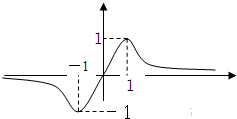
【答案解析】根据图象可知f(1)=1,f(0)=0,f′(1)=0
∴b=0
f′(x)=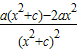 =
=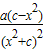
∵f′(1)=0∴a(c-1)=0
而f(1)=1=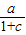
∴a=2,c=1
∴a>c>b
故答案为:a>c>b
先根据函数图象得到f(1)=1,f(0)=0,f′(1)=0,建立等式关系,求出a、b、c的值,即可比较它们的大小.
33 .
函数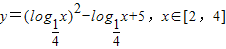 的值域为 .
的值域为 .
【答案解析】令t=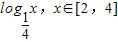 ,则-1≤t≤-
,则-1≤t≤- .
.
∴y=t2-t+5=(t- )2+
)2+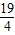 ,-1≤t≤-
,-1≤t≤- .
.
∴ymax=7,ymin=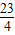 ,∴函数的值域为
,∴函数的值域为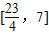
故答案为: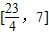 .
.
根据题意,令t=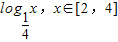 ,利用对数函数的单调性,求出t的范围,转化为二次函数y=t2-t+5在区间,[-1,-
,利用对数函数的单调性,求出t的范围,转化为二次函数y=t2-t+5在区间,[-1,- ]上的最值问题,采用配方法即可求得结果.
]上的最值问题,采用配方法即可求得结果.
34 .
已知集合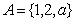 与集合
与集合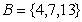 ,若
,若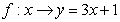 是从
是从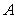 到
到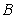 的映射则
的映射则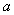 的值为_________________.
的值为_________________.
【答案解析】4
35 .
定义区间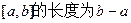 ,区间
,区间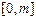 在映射
在映射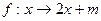 所得的对应区间为
所得的对应区间为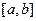 ,若区间
,若区间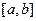 的长度比区间
的长度比区间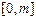 的长度大5,则m= _ .
的长度大5,则m= _ .
【答案解析】5
36 .
已知函数![]() 满足:
满足:![]() ,
,![]() ,则
,则![]() _____
_____
【答案解析】4020。提示:![]() =2,且
=2,且![]()
![]()
![]()
![]() =4020
=4020
37 .
已知函数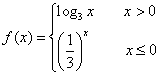 ,则不等式
,则不等式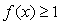 的解集为_____________.
的解集为_____________.
【答案解析】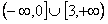
38 .
规定满足“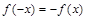 ”的分段函数
”的分段函数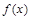 叫做“对偶函数”,已知函数
叫做“对偶函数”,已知函数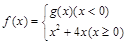 是“对偶函数”,则(1)
是“对偶函数”,则(1)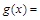 ;
;
(2)若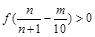 对任意正整数
对任意正整数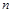 都成立,实数
都成立,实数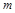 的取值范围为 .
的取值范围为 .
【答案解析】(1)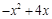 ;(2)
;(2)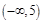
39 .
设S,T是R的两个非空子集,如果存在一个从S到T的函数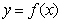 满足:
满足:
(i)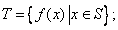 (ii)对任意
(ii)对任意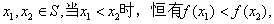
那么称这两个集合“保序同构”,现给出以下3对集合:
①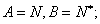
②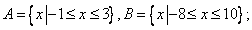
③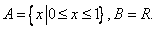
其中,“保序同构”的集合对的序号是_______。(写出“保序同构”的集合对的序号)。
【答案解析】①②③
40 .
集合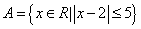 中最小整数位 .
中最小整数位 .
【答案解析】![]()
![]() 不等式
不等式![]() ,即
,即![]() ,
,![]() ,所以集合
,所以集合![]() ,所以最小的整数为
,所以最小的整数为![]() 。
。
41 .
下面四个命题:
①函数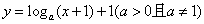 的图象必经过定点(0,1);
的图象必经过定点(0,1);
②已知命题 :
: ,则
,则 :
: ;
;
③过点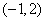 且与直线
且与直线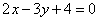 垂直的直线方程为
垂直的直线方程为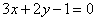 ;
;
④在区间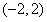 上随机抽取一个数
上随机抽取一个数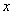 ,则
,则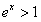 的概率为
的概率为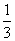 。
。
其中所有正确命题的序号是:_____________。
【答案解析】①③
当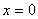 时,
时,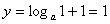 ,所以恒过定点
,所以恒过定点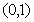 ,所以①正确;命题
,所以①正确;命题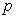 的否定为:
的否定为: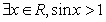 ,所以②错误;直线
,所以②错误;直线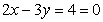 的斜率为
的斜率为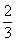 ,所以和
,所以和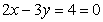 垂直的直线斜率为
垂直的直线斜率为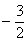 ,因为直线过点
,因为直线过点 ,所以所求直线方程为
,所以所求直线方程为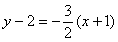 ,即
,即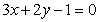 ,所以③正确;由
,所以③正确;由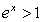 得,
得,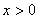 ,所以相应的概率为
,所以相应的概率为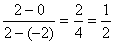 ,所以④错误,所以正确的命题有①③。
,所以④错误,所以正确的命题有①③。
42 .
设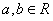 ,集合
,集合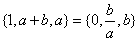 ,则
,则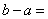 .
.
【答案解析】2
43 .
设A是整数集的一个非空子集,对于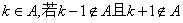 ,则k是A的一个“孤立元”,给定
,则k是A的一个“孤立元”,给定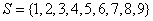 ,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。
,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。
【答案解析】7
44 .
平面点集![]() ,用列举法表示
,用列举法表示![]() 。
。
【答案解析】![]()
45 .
在平面直角坐标系中,定义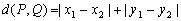 为两点
为两点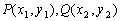 之间的“折线距离”,在这个定义下,给出下列命题:
之间的“折线距离”,在这个定义下,给出下列命题:
①到原点的“折线距离”等于1 的点的集合是一个正方形;
②到原点的“折线距离”等于1 的点的集合是一个圆;
③到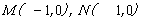 两点的“折线距离”之和为4的点的集合是面积为6的六边形;
两点的“折线距离”之和为4的点的集合是面积为6的六边形;
④到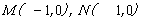 两点的“折线距离”差的绝对值为1的点的集合是两条平行线;
两点的“折线距离”差的绝对值为1的点的集合是两条平行线;
其中正确的命题是 。(写出所有正确命题的序号)
【答案解析】①③④
46 .
已知集合![]() ,且关于x的方程
,且关于x的方程![]() 有唯一实数解,用列举法表示集合
有唯一实数解,用列举法表示集合![]() 为 .
为 . ![]()
【答案解析】![]()
47 .
集合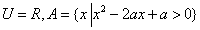 ,如果
,如果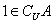 ,那么
,那么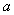 的取值范围是_____.
的取值范围是_____.
【答案解析】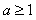
48 .
已知函数f(x)的定义域为R,则下列命题中:
①若f(x-2)是偶函数,则函数f(x)的图象关于直线x=2对称;②若f(x+2)=-f(x-2),则函数f(x)的图象关于原点对称;③函数y=f(2+x)与函数y=f(2-x)的图象关于直线x=2对称;④函数y=f(x-2)与函数y=f(2-x)的图象关于直线x=2对称.
其中正确的命题序号是 .
【答案解析】④
解:①不正确.因为f(x-2)的图象是由f(x)的图象向右平移两个单位而得到,结合f(x-2)是偶函数知,f(x)的图象关于x=-2对称,
②由f(x+2)=-f(x-2)变形得f(x+8)=f(x)是周期函数.不能得出函数f(x)的图象关于原点对称,故不正确.
③不正确,因为函数y=f(2+x)是由f(x)向左平移2个单位,函数y=f(2-x)的图象是由f(-x)的图象向右平移2个单位,故两函数的图象仍然关于原点对称.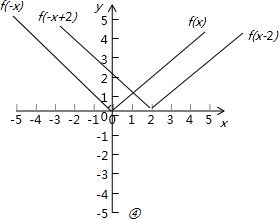
④如图所示,正确.
故答案为:④
49 .
下列5个判断:
①若f(x)=x2-2ax在[1,+∞)上增函数,则a=1;
②函数y=2x-1与函数y=log2(x+1)的图象关于直线y=x对称;
③函数y=In(x2+1)的值域是R;
④函数y=2|x|的最小值是1;
⑤在同一坐标系中函数y=2x与y=2-x的图象关于y轴对称.
其中正确的是 .
【答案解析】②④⑤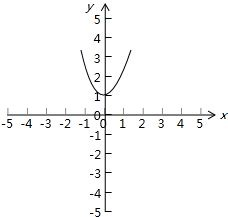 解:①若f(x)=x2-2ax在[1,+∞)上增函数,则a≤1;不正确.
解:①若f(x)=x2-2ax在[1,+∞)上增函数,则a≤1;不正确.
②解函数y=2x-1的反函数为y=log2(x+1),所以其图象关于直线y=x对称;正确.
③∵x2+1≥1,所以其值域是[0,+∞);不正确.
④作出函数y=2|x|的图象,如图所示,正确.
⑤在同一坐标系中函数y=2x与y=2-x的图象情境如④,可知关于y轴对称.正确.
故答案为:②④⑤
50 .
在平面直角坐标系中,若点A、B同时满足
(1)点A、B都在函数y=f(x)的图象上;
(2)点A、B关于原点对称.则称点对(A,B)是函数y=f(x)的一个“姐妹点对”(规定点对(A,B)与点对(B,A)是同一个“姐妹点对”).若函数f(x)=ax-x-a(a>0且a≠1)只有一个“姐妹点对”,则a的取值范围为 .
【答案解析】a>1
解:构建函数y=ax(a>0,且a≠1)和函数y=x+a,函数y=ax(a>0,且a≠1)关于原点对称的函数为y=-a-x
∵函数f(x)=ax-x-a(a>0且a≠1)只有一个“姐妹点对”,
∴函数y=x+a与y=a-x只有一个交点
∵a>1时,y=a-x单调减,与函数y=x+a图象只有一个交点;
0<a<1时,y=a-x单调减,与函数y=x+a图象没有交点;
此时有a>1;
故答案为a>1.