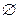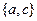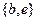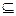 A,则这样的集合B一共有( )
A,则这样的集合B一共有( )
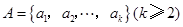 ,其中
,其中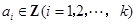 ,由
,由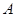 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: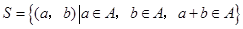 ,
,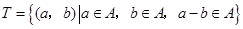 .其中
.其中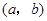 是有序数对,集合
是有序数对,集合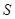 和
和 中的元素个数分别为
中的元素个数分别为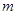 和
和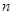 .若对于任意的
.若对于任意的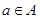 ,总有
,总有 ,则称集合
,则称集合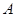 具有性质
具有性质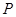 .
.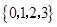 与
与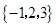 是否具有性质
是否具有性质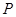 并对其中具有性质
并对其中具有性质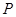 的集合,写出相应的集合
的集合,写出相应的集合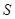 和
和 ;
;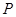 的集合
的集合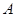 ,证明:
,证明: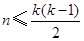 ;
;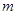 和
和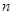 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
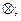 当m、n都是正偶数或都是正奇数时,
当m、n都是正偶数或都是正奇数时, 当
当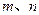 中一个为正奇数另一个为正偶数时,
中一个为正奇数另一个为正偶数时,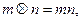 则集合
则集合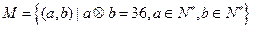 中的元素个数是 (
中的元素个数是 ( )
)

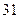
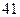
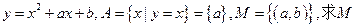
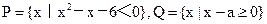
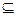 Q,求实数a的取值范围.
Q,求实数a的取值范围.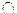 Q=
Q=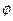 ,求实数a的取值范围
,求实数a的取值范围
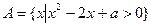 ,且
,且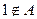 ,则实数
,则实数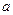 的取值范围是
的取值范围是
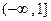
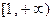
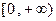
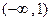
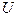 ,集合
,集合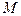 和
和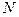 满足
满足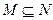 ,则下列结论中不成立的是
,则下列结论中不成立的是
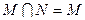
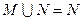
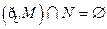
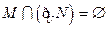
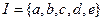 ,集合
,集合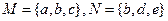 ,那么
,那么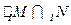 是( )
是( )