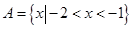 ,
,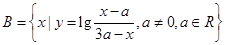 .
.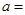 1时,求集合
1时,求集合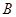 ;
;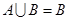 时,求
时,求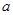 的取值范围.
的取值范围.
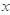 ,
,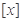 表示不超过
表示不超过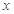 的最大整数,如
的最大整数,如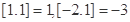 .定义在
.定义在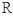 上的函数
上的函数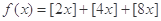 ,若
,若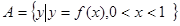 ,则
,则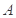 中元素的最大值与最小值之和为( )
中元素的最大值与最小值之和为( )
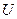 ,用集合
,用集合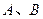 的交集、并集、补
的交集、并集、补 集分别表示右边韦恩图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分为:Ⅰ部分:
集分别表示右边韦恩图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分为:Ⅰ部分: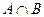 ,Ⅱ部分:
,Ⅱ部分: ,Ⅲ部分:
,Ⅲ部分: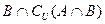 ,Ⅳ部分:
,Ⅳ部分: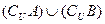 ,其中表
,其中表 示错误的是 ( )
示错误的是 ( )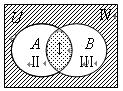
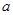 -1,
-1,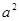 },B={
},B={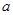 -5,1-
-5,1-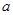 ,9},分别求适合下列条件的
,9},分别求适合下列条件的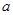 的值.
的值.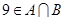 ;
;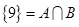 .
.
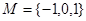 ,
,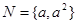 则使M∩N=N成立的
则使M∩N=N成立的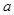 的值是( )
的值是( )
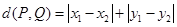 为两点
为两点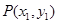 ,
,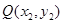 之间的“折线距离”.在这个定义下,给出下列命题:
之间的“折线距离”.在这个定义下,给出下列命题: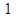 的点的集合是一个正方形;
的点的集合是一个正方形;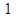 的点的集合是一个圆;
的点的集合是一个圆;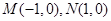 两点的“折线距离”相等的点的轨迹方程是
两点的“折线距离”相等的点的轨迹方程是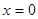 ;
;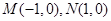 两点的“折线距离”差的绝对值为
两点的“折线距离”差的绝对值为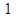 的点的集合是两条平行线.其中正确的命题有( )
的点的集合是两条平行线.其中正确的命题有( )
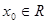 满足:对任意
满足:对任意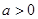 ,都存在
,都存在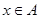 使得
使得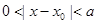 ,则称
,则称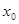 为集合A的聚点.用Z表示整数集,则在下列集合中,以0为聚点的集合有( )
为集合A的聚点.用Z表示整数集,则在下列集合中,以0为聚点的集合有( )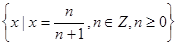 (2)不含0的实数集R
(2)不含0的实数集R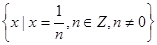 (4)整数集Z
(4)整数集Z
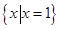
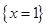
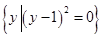
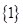
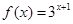 是指数函数;
是指数函数;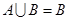 ,则
,则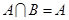
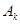 :(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为
:(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为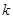
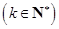 的等差数列.那么
的等差数列.那么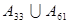 中元素的个数是( )
中元素的个数是( )