 .
. 的值;
的值;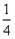 ,b=2, 求△ABC的面积S.
,b=2, 求△ABC的面积S. 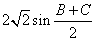 ,2sinA),若m∥n,|p|2=9,试判断△ABC的形状。
,2sinA),若m∥n,|p|2=9,试判断△ABC的形状。 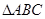 中,内角
中,内角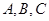 的对边分别为
的对边分别为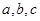 . 已知
. 已知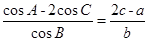 .
. 的值; (2) 若
的值; (2) 若 ,求
,求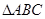 的面积.
的面积. 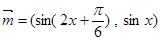 ,
,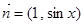 ,
,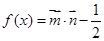 .
.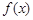 的单调递减区间;
的单调递减区间;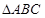 中,
中,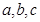 分别是角
分别是角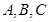 的对边,
的对边, ,
,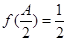 ,
,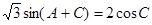 ,求
,求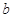 的大小.
的大小. 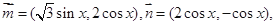 函数
函数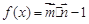 .
. 的最小正周期和对称轴的方程;
的最小正周期和对称轴的方程; 的角
的角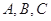 的对边分别为
的对边分别为 ,且
,且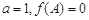 ,求
,求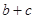 的取值范围.
的取值范围. 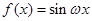
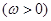 在区间
在区间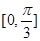 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形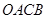 中,
中, ,
,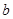 ,
,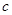 为
为 的内角
的内角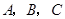 的对边,
的对边, .
.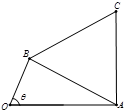
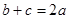 ;
;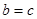 ,设
,设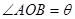 ,
,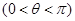 ,
,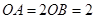 ,求四边形
,求四边形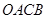 面积的最大值.
面积的最大值. 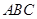 中,角
中,角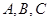 的对边分别为
的对边分别为 ,已知
,已知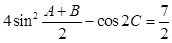 ,且
,且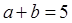 ,
,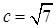 ,
,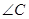 (2)△
(2)△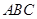 的面积.
的面积. 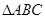 中,角
中,角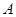 、
、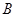 、
、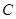 所对的边分别为
所对的边分别为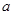 、
、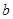 、
、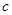 .已知
.已知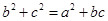 .
.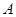 的大小;
的大小; ,
, ,求
,求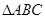 的面积.
的面积. 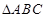 中,
中,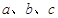 分别为角
分别为角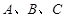 的对边,△ABC的面积S满足
的对边,△ABC的面积S满足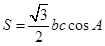 .
.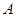 的值;
的值; ,设角
,设角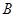 的大小为
的大小为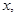 用
用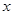 表示
表示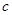 ,并求
,并求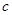 的取值范围.
的取值范围. 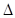
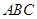 中,内角
中,内角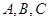 的对边分别为
的对边分别为 .已知
.已知 .
.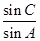 的值; (Ⅱ)若
的值; (Ⅱ)若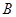 为钝角,
为钝角,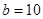 ,求
,求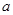 的取值范围.
的取值范围.