首页 请复制到word或wps中编辑使用(ctrl+c,ctrl+v),vip用户页面底部可看到答案解析 公式上下对齐方法复制内容

八上数学第十三章综合试题

一.单选题 (共 10 小题)

1 . (如图)被长方形盖住的图形，可能是(　　)三角形。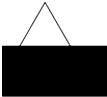

A、锐角
B、直角
C、钝角
D、都有可能

2 . 在一个三角形中，∠1-∠2=∠3，那么这个三角形一定是[     ](     )

A、锐角三角形
B、钝角三角形
C、直角三角形
D、等边三角形

3 . 在钝角三角形里面可以作出几条高？[     ](     )

A、1条
B、2条
C、3条
D、无数条

4 . 一个三角形的三个内角的度数比是1：2：3，按角分这是一个(　　)

A、锐角三角形
B、直角三角形
C、钝角三角形
D、无法确定

5 . 在△ABC中，若∠A=95°，∠B=40°，则∠C的度数为(　　)

A、35°
B、40°
C、45°
D、50°

6 . 下面是小强用三根火柴组成的图形，其中符合三角形概念的是(　　)

A、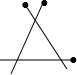
B、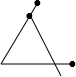
C、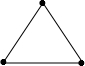
D、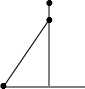

7 . 如图，三角形的个数是(　　)

A、4
B、6
C、8
D、10

8 . 已知△ABC的一个外角为50°，则△ABC一定是(　　)

A、锐角三角形
B、钝角三角形
C、直角三角形
D、锐角三角形或钝角三角形

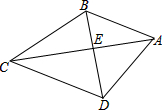
9 . 如图，在直角三角形ABC中，AC≠AB，AD是斜边BC上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C(除之C外)相等的角的个数是( )

A、2
B、3
C、4
D、5

10 . 直角三角形斜边上的中点是( )

A、三条边中线的交点
B、三边高线的交点
C、三个角平分线的交点
D、三边中垂线的交点

二.填空题 (共 6 小题)

1 . 下图中有(    )个直角三角形，有(    )个锐角三角形，有(    )个钝角三角形，有(    )个等腰三角形。

2 . 一个n边形有         个顶点，         条边，         个内角，         个外角．

3 . 如图，把边长为b的等边三角形的纸板剪去三个三角形，得到正六边形，则正六边形的周长为(    )。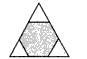

4 . 如右图所示，在△ABC中，AB＝AC，∠BAD＝24^o，AD＝AE，则∠EDC＝   。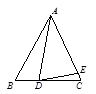

5 . 一个角是80°的等腰三角形的另两个角为         .

6 . 三角形纸片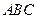中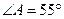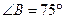，，，将纸片的一角折叠，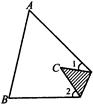

使点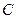落在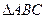内(如图)，
则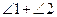的度数为_______________。

三.解答题 (共 3 小题)

1 . 课本拓展
旧知新意：
我们容易证明，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？
1.尝试探究：
(1)如图1，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC＋∠ECB之间存在怎样的数量关系？为什么？[来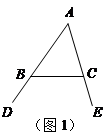

2.初步应用：
(2) 如图2，在△ABC纸片中剪去△CED，得到四边形ABDE，∠1＝130°，
则∠2－∠C＝_______________；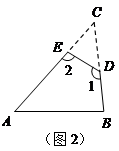

(3) 小明联想到了曾经解决的一个问题：如图3，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请利用上面的结论直接写出答案_                  _．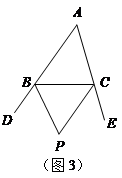

3.拓展提升：
(4) 如图4，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A、∠D有何数量关系？为什么？(若需要利用上面的结论说明，可直接使用，不需说明理由．)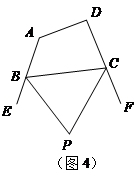

2 . 如图，△ABC中，AD是BC上的高，AE平分∠BAC，∠B=75°，∠C=45°，求∠DAE与∠AEC的度数.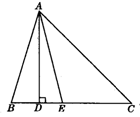

3 . ∠1=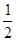∠2，∠1+∠2=162°，求∠3与∠4的度数．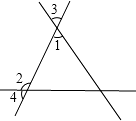

答案和解析(vip用户才显示)