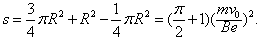首页 请复制到word或wps中编辑使用(ctrl+c,ctrl+v),vip用户页面底部可看到答案解析 公式上下对齐方法
磁场偏转
一.单选题
(共 3 小题)
1 .
如图所示,MN是一荧光屏,当带电粒子打到荧光屏上时,荧光屏能够发光MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里,P为屏上的一小孔,PQ与MN垂直一群质量为m、带电荷量q的粒子(不计重力),以相同的速率v,从P点沿垂直于磁场方向射入磁场区域,其入射方向分布在以PQ为中心,夹角为2θ的范围内,不计粒子间的相互作用,以下说法正确的是()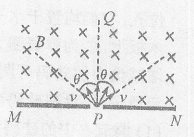
A、荧光屏上将出现一圆形亮斑,其半径为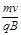
B、荧光屏上将出现一条亮线,其长度为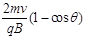
C、荧光屏上将出现一条亮线,其长度为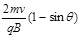
D、荧光屏上将出现一条亮线,其最右端距P点为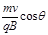
【答案解析】B
2 .
如图所示,半径为r的圆形空间内,存在着垂直于纸面向里的匀强磁场,一个带电粒子(不计重力),从A点以速度v0垂直磁场方向射入磁场中,并从B点射出,∠AOB=1200,则该带电粒子在磁场中运动的时间为()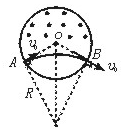
A、2πr/3v0
B、2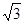 πr/3v0
πr/3v0
C、πr/3v0
D、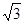 πr/3v0
πr/3v0
【答案解析】D
3 .
如图所示,沿直线通过速度选择器的正离子从狭缝S射入磁感应强度为B2的匀强磁场中,偏转后出现的轨迹半径之比为R1∶R2=1∶2,则下列说法正确的是( )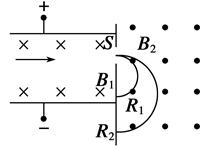
A、离子的速度之比为1∶2
B、离子的电荷量之比为1∶2
C、离子的质量之比为1∶2
D、以上说法都不对
【答案解析】D
二.多选题
(共 3 小题)
1 .
如图所示,在ab=bc的等腰三角形abc区域内有垂直纸面向外的匀强磁场,d是ac上任意一点,e是bc上任意一点大量相同的带电粒子从a点以相同方向垂直磁场射入,由于速度大小不同,粒子从ac和bc上不同点离开磁场不计粒子重力,则从c点离开的粒子在三角形abc磁场区域内经过的弧长和运动时间与从d点和e点离开的粒子相比较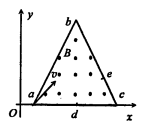
A、经过的弧长一定大于从d点离开的粒子经过的弧长
B、经过的弧长一定小于从e点离开的粒子经过的弧长
C、运动时间一定大于从d点离开的粒子的运动时间
D、运动时间一定大于从e点离开的粒子的运动时间
【答案解析】A,D
2 .
在一个边界为等边三角形的区域内,存在一个方向垂直于纸面向内的匀强磁场,在磁场边界上的P点处有一个粒子源,发出比荷相同的三个粒子a、b、c(不计重力)沿同一方向进入磁场,三个粒子通过磁场的轨迹如图所示,用ta、tb、tc分别表示a、b、c通过磁场的时间;用ra、rb、rc分别表示a、b、c在磁场中的运动半径,则下列判断正确的是
A、ta=tb>tc
B、tc>tb>ta
C、rc>rb>ra
D、rb>ra>rc
【答案解析】A,C
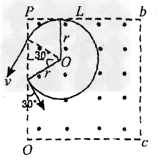
3 . 如图所示,正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,三个完全相同的带电粒子a、b、c分别以大小不同的初速度va、vb、vc从A点沿图示方向射入该磁场区域,经磁场偏转后粒子a、b、c分别从BC边中点、CD边中点、AD边中点射出若ta、tb、tc分别表示粒子a、b、c在磁场中的运动时间则以下判断正确的是( )
A、va<vb<vc
B、vc<vb<va
C、ta<tb<tc
D、ta=tb<tc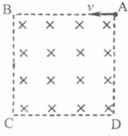
【答案解析】B,C
三.解答题
(共 24 小题)
1 .
如图, OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C(
OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C(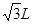 ,0),在
,0),在 OAC区域内有垂直于xOy平面向里的匀强磁场。在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴。不计粒子重力和空气阻力及粒子间相互作用。
OAC区域内有垂直于xOy平面向里的匀强磁场。在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴。不计粒子重力和空气阻力及粒子间相互作用。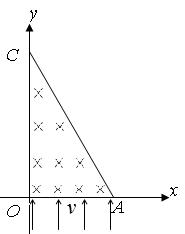
(1)求磁场的磁感应强度B的大小;
(2)若从OA边两个不同位置射入磁场的粒子,先后从OC边上的同一点P(P点图中未标出)射出磁场,求这两个粒子在磁场中运动的时间t1与t2之间应满足的关系;
(3)从OC边上的同一点P射出磁场的这两个粒子经过P点的时间间隔与P点位置有关,若该时间间隔最大值为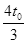 ,求粒子进入磁场时的速度大小。
,求粒子进入磁场时的速度大小。
【答案解析】(1)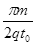 (2)t1+ t2=
(2)t1+ t2=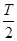 =2t0 (3)
=2t0 (3)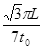
(1) 粒子在t0时间内,速度方向改变了90°,故周期
T=4t0 ①
由T=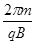 得B=
得B=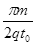 ②
②
(2)在同一点射出磁场的两粒子轨迹如图,轨迹所对应的圆心角分别为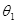 和
和 ,由几何关系有
,由几何关系有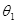 =180°-
=180°- ③
③
故t1+ t2=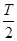 =2t0 ④
=2t0 ④ 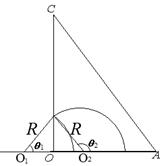
(3)由圆周运动知识可知,两粒子在磁场中运动的时间差 t与
t与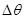 =
= -
-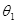 成正比,由③得
成正比,由③得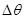 =
= -
-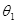 =2
=2 -180° ⑤
-180° ⑤
根据⑤式可知 越大,时间差
越大,时间差 t越大由
t越大由 t=
t=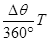 ⑥
⑥
由③及题意代入数据得 的最大值为
的最大值为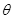 =150° ⑦
=150° ⑦
在磁场中运动时间最长的粒子轨迹如图,由几何关系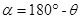 =30° ⑧
=30° ⑧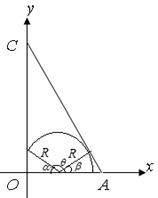
tan∠A=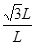 =
=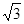 得∠A=60° ⑨
得∠A=60° ⑨ 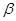 =90°-∠A=30° ⑩
=90°-∠A=30° ⑩ 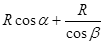 =L ⑪ 解得R=
=L ⑪ 解得R=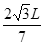 ⑫
⑫
根据qvB=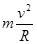 ⑬ 代入数据解得 v=
⑬ 代入数据解得 v=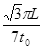 ⑭
⑭
2 .
如图所示,两块平行金属板M、N正对着放置,s1、s2分别为M、N板上的小孔 ,s1、s2、O三点共线,它们的连线垂直M、N,且s2O=R..以O为圆心、R为半径的圆形区域内同时存在磁感应强度为B、方向垂直纸面向外的匀强磁场和电场强度为E的匀强电场.D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板。质量为m、电荷量为+q的粒子,经s1进入M、N间的电场后,通过s2进入电磁场区域,然后沿直线打到光屏P上的s3点.粒子在s1处的速度和粒子所受的重力均不计.求:
,s1、s2、O三点共线,它们的连线垂直M、N,且s2O=R..以O为圆心、R为半径的圆形区域内同时存在磁感应强度为B、方向垂直纸面向外的匀强磁场和电场强度为E的匀强电场.D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板。质量为m、电荷量为+q的粒子,经s1进入M、N间的电场后,通过s2进入电磁场区域,然后沿直线打到光屏P上的s3点.粒子在s1处的速度和粒子所受的重力均不计.求: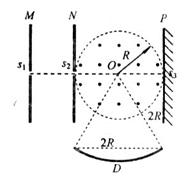
小题1:M、N两板间的电压为R;
小题2:撤去圆形区域内的电场后,当M、N间的电压改为U1时,粒子恰好垂直打在收集板D的中点上,求电压U1的值及粒子在磁场中的运动时间t;
小题3:撤去圆形区域内的电场后,改变M、N间的电压时,粒子从s2运动到D板经历的时间t会不同,求t的最小值。
【答案解析】小题1: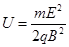
小题2: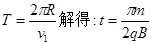
小题3: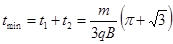
(1)正粒子沿直线打到P板上的s3点,可知: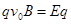 ……………(1分)
……………(1分)
粒子在M、N间的电场加速满 足
足 :
: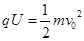 ……………………………………(1分)
……………………………………(1分)
得: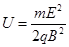 …………………………………………………………………………(1分)
…………………………………………………………………………(1分)
(2)粒子恰好打在收集板D的中点上,粒子在磁场中做圆周运动的半径为R由牛顿第 二定律可知:
二定律可知: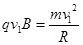 ………………………………………………………………(1分)
………………………………………………………………(1分)
又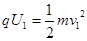 …………………………………………………………………………(1分)
…………………………………………………………………………(1分)
得: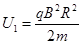 …………………………………………………………………………(1分)
…………………………………………………………………………(1分)
粒子在磁场中做圆周运动的时间为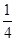 周期,由
周期,由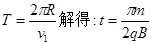 …………(1分)
…………(1分)
(3)M、N间的电压越大,粒子进入磁场时的速度越大,粒子在磁场中运动轨迹的半径越大,在磁场中运动的时间也会越短,出磁场后匀速运动的时间也越短,所以当粒子 打在收集板D的右端时,对应时间t最短。
打在收集板D的右端时,对应时间t最短。
根据几何关系可以求得粒子在磁场中运动的半径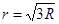 …………………………(1分)
…………………………(1分)
粒子在磁场中运动的时间为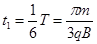 …………………………………………(1分)
…………………………………………(1分)
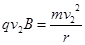 ……………………………………………………………………………(1分)
……………………………………………………………………………(1分)
粒子出磁场后做匀速直线运动经历的时间: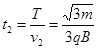 ………(1分)
………(1分)
粒子经过s2后打在D上t的最小值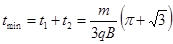 …(1分)
…(1分)
3 .
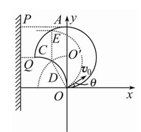
如图所示,xOy坐标系的第一象限内,有一边界线OA与y轴的夹角∠AOy=45O,边界线的上方与下方分别存在垂直纸面向外与向里的匀强磁场,磁感应强度大小均为B=0.25T.一束带电量q=8.0×10-19C、质量 m=8.0×10-26kg的正离子以v=5×105m/s从y轴上坐标为(0,0.4m)的Q点垂直y轴射入磁场区。求: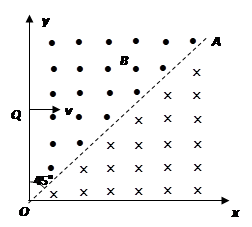
(1)离子在磁场中做圆周运动的半径和周期;
(2)现只改变B的大小,使离子不经过OA边界而直接从y轴离开磁场区域,则B应满足什么条件?
(3)若B=0.125T,且从离子经过Q点开始计时,则离子在哪些时刻恰好经过OA边界?
【答案解析】(1)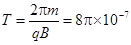 s (2)
s (2)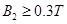 (3)
(3)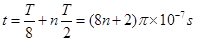
(1)洛伦兹力提供向心力 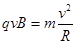 (2分)
(2分)
解得: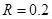 m (1分,若直接
m (1分,若直接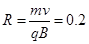 m,给3分)
m,给3分)
周期为: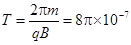 s (3分:公式2分,结果1分)
s (3分:公式2分,结果1分)
(2)临界条件是:在AOy区间的运动轨迹恰好与OA相切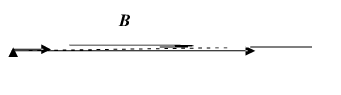
则: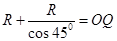 (3分,不写此式但画图正确也给分)
(3分,不写此式但画图正确也给分)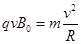
解得: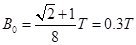
所以B2应该满足: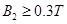
(3)如果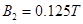 ,则离子在两个磁场做圆周运动的周期和半径分别为:
,则离子在两个磁场做圆周运动的周期和半径分别为: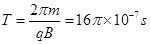
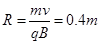
由几何关系得:离子从Q点进入AOy经过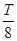 后,垂直OA边进入AOx区域,
后,垂直OA边进入AOx区域,
再经过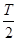 后垂直OA边界进入AOy区域,
后垂直OA边界进入AOy区域,
再经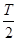 后又垂直OA边界进入AOx区域……
后又垂直OA边界进入AOx区域……
所以离子恰好经过OA边界的时刻为: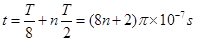
4 .
一匀强磁场分布在以O为圆心,半径为R的圆形区域内,方向与纸面垂直,如图所示,质量为m、电荷量q的带正电的质点,经电场加速后,以速度v沿半径MO方向进入磁场,沿圆弧运动到N点,然后离开磁场,∠MON=120º,质点所受重力不计,求: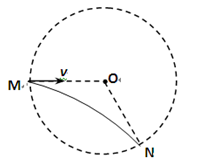
(1)判断磁场的方向;
(2)该匀强磁场的磁感应强度B;
(3)带电质点在磁场中运动的时间。
【答案解析】(1)垂直纸面向外 (2)B=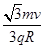 (3)t=
(3)t=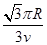
(1)根据左手定则,可知该磁场方向垂直纸面向外;
(2)粒子在磁场中做匀速圆周运动,设轨道半径为r,圆心为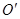 如图所示,洛仑兹力提供向心力
如图所示,洛仑兹力提供向心力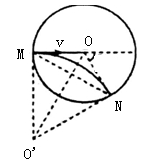
因此: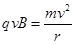
由几何关系可得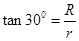
联立得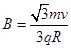
(3)设粒子在磁场中运动的时间为t,粒子做匀速圆周运动,期周期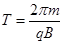
由于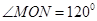 ,因此运动的圆心角
,因此运动的圆心角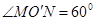
因此粒子在磁场中运动的时间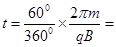
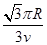
5 .
如图所示,在光滑绝缘的水平面内,对角线AC将边长为L的正方形分成ABC和ADC两个区域,ABC区域有垂直于水平面的匀强磁场,ADC区域有平行于DC并由C指向D的匀强电场.质量为m、带电量为+q的粒子从A点沿AB方向以v的速度射入磁场区域,从对角线AC的中点O进入电场区域.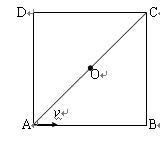
(1)判断磁场的方向并求出磁感应强度B的大小.
(2)讨论电场强度E在不同取值时,带电粒子在电场中运动的时间t.
【答案解析】(1)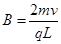 ,方向垂直纸面向里 (2)(i)当
,方向垂直纸面向里 (2)(i)当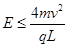 时,
时,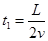 ,(ii)当
,(ii)当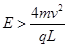 时,
时,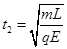
(1)根据左手定则,可以判断磁场方向垂直纸面向里。
设带电粒子在磁场中运动的半径为r,有: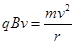
依题意,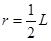 联立,解得:
联立,解得: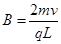
(2)粒子进入电场的速度沿竖直方向,在电场中做类平抛运动,竖直方向匀速直线运动,水平方向匀加速直线运动
设带电粒子恰好从D点离开电场时对应的电场强度为E0,则有竖直方向: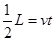
水平方向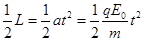 得:
得: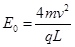
讨论:(i)当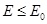 时,粒子从DC边离开电场,此时粒子在电场中运动的时间为
时,粒子从DC边离开电场,此时粒子在电场中运动的时间为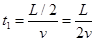
(ii)当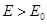 时,粒子从AD边离开电场,此时粒子在电场中运动的时间为t2,有:
时,粒子从AD边离开电场,此时粒子在电场中运动的时间为t2,有: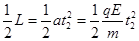 得:
得: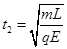
6 .
如图所示,虚线所围圆形区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B.一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成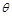 角.设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力.求:
角.设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力.求:
(1)电子在磁场中运动的时间t
(2)圆形磁场区域的半径r.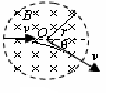
【答案解析】(1)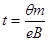 (2)
(2)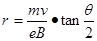
1)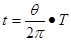
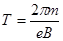
解得: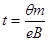
(2) 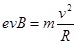
由几何关系得: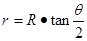
解得: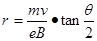
点评:需要注意的是粒子在磁场中的运动和速度无关,只和轨迹所对的圆心角有关
7 .
如图所示,质量为m,电荷量为e的电子从坐标原点O处沿xOy平面射入第一象限内,射入时的速度方向不同,但大小均为v0.现在某一区域内加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度大小为B,若这些电子穿过磁场后都能垂直地射到与y轴平行的荧光屏MN上,求: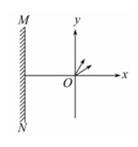
小题1:电子从y轴穿过的范围;
小题2:荧光屏上光斑的长度;
小题3:所加磁场范围的最小面积.
【答案解析】小题1: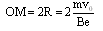
小题2: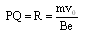
小题3: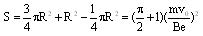
(1)设粒子在磁场中运动的半径为R,由牛顿第二定律得: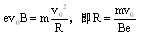
电子从y轴穿过的范围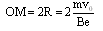
(2)如图所示,初速度沿x轴正方向的电子沿弧OA运动到荧光屏MN上的P点,
初速度沿y轴正方向的电子沿弧OC运动到荧光屏MN上的Q点
由几何知识可得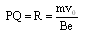
(3)取与x轴正方向成θ角的方向射入的电子为研究对象,其射出磁场的点为E(x,y),因其射出后能垂直打到荧光屏MN上,故有:
x="-Rsinθ "
y="R+Rcosθ "
即x2+(y-R)2=R2
又因为电子沿x轴正方向射入时,射出的边界点为A点;沿y轴正方向射入时,射出的边界点为C点,故所加最小面积的磁场的边界是以(0,R)为圆心、R为半径的圆的一部分,如图中实线圆弧所围区域,所以磁场范围的最小面积为: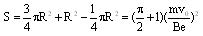
8 .
甲图为质谱仪的原理图.带正电粒子从静止开始经过电势差为U的电场加速后,从G点垂直于MN进入偏转磁场.该偏转磁场是一个以直线MN为上边界、方向垂直于纸面向外的匀强磁场,磁场的磁感应强度为B,带电粒子经偏转磁场后,最终到达照相底片上的H点.测得G、H间的距离为d,粒子的重力忽略不计.
(1)设粒子的电荷量为q,质量为m,试证明该粒子的比荷为: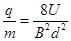 ;
;
(2)若偏转磁场的区域为圆形,且与MN相切于G点,如图乙所示,其它条件不变。要保证上述粒子从G点垂直于MN进入偏转磁场后不能打到MN边界上(MN足够长),求磁场区域的半径应满足的条件。
【答案解析】(1)证明见解析(2)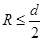
(1)粒子经过电场加速,设进入磁场速度v,由动能定理可得: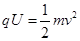 (3分)
(3分)
进入磁场后做圆周运动,设轨迹半径为r,则有: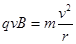 (3分)
(3分)
打到H点时,由几何关系可得: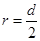 (2分)
(2分)
联立以上各式,解得: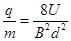 (2分)
(2分)
(2)要保证所有粒子都不能打到MN边界上,粒子在磁场中运动偏转角小于等于900,偏转角度恰好等于900,如图所示,此时磁场区半径为: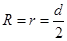 (3分)
(3分)
所以磁场半径满足: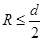 (2分)
(2分)
9 .
如图在第一象限存在匀强磁场,第四象限存在正交电场和磁场,磁感应强度均为B,一个电子从y轴上的c点平行x轴射入磁场,经x轴的P点沿PC直线射出第四象限,已知AC的长度为L;∠CAP=30°;电子质量为m,电量为q。求: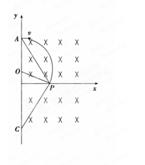
(1)电子射入磁场时的速度v;
(2)电子在第一象限运动时间;
(3)电场强度E的大小和方向;
(4)电子在第四象限运动时间.
【答案解析】(1)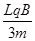 (2)
(2)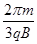 (3)
(3)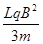 ,30°(4)
,30°(4)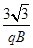
分析如图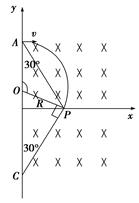
(1)设电子在第一象限做圆周运动的半径为R,由几何知识得∠ACP=30° OC=2OP
又OP=R ,OC=L-R;(2分)所以L-R=2R;R=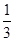 L(2分)
L(2分)
由qvB=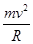 得v=
得v=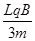 (2分)
(2分)
(2) 由几何知识得,电子在第一象限做圆周运动转过的圆心角α=120°=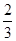 π(2分)
π(2分)
电子在第一象限运动时间t1=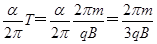 (2分)
(2分)
(3)由qE=qvB得E=vB=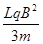 (2分)
(2分)
由二力平衡知,电场强度的方向在纸面内斜向下与x轴成30°(2分)
(4)电子在第四象限运动时间为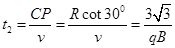
10 .
钍核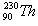 发生衰变生成镭核
发生衰变生成镭核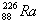 并放出一个粒子。设该粒子的质量为m、电荷量为q,它进入电势差为U的带窄缝的平行平板电极S1和S2间电场时,其速度为v0,经电场加速后,沿ox方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,ox垂直平板电极S2,当粒子从p点离开磁场时,其速度方向与ox方位的夹角θ=60°,如图所示,整个装置处于真空中。
并放出一个粒子。设该粒子的质量为m、电荷量为q,它进入电势差为U的带窄缝的平行平板电极S1和S2间电场时,其速度为v0,经电场加速后,沿ox方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,ox垂直平板电极S2,当粒子从p点离开磁场时,其速度方向与ox方位的夹角θ=60°,如图所示,整个装置处于真空中。
(1)写出钍核衰变方程;
(2)求粒子在磁场中沿圆弧运动的轨道半径R;
(3)求粒子在磁场中运动所用时间t。 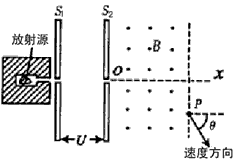
【答案解析】(1)钍核衰变方程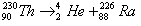 ①
①
(2)设粒子离开电场时速度为v,对加速过程有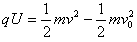 ②
②
粒子在磁场中有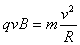 ③
③
由②、③得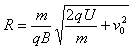 ④
④
(3)粒子做圆周运动的回旋周期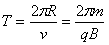 ⑤
⑤
粒子在磁场中运动时间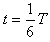 ⑥
⑥
由⑤、⑥得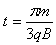 ⑦
⑦
11 .
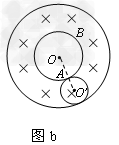
在真空中,半径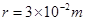 的圆形区域内有匀强磁场,方向如图所示,磁感应强度B="0.2" T,一个带正电的粒子以初速度
的圆形区域内有匀强磁场,方向如图所示,磁感应强度B="0.2" T,一个带正电的粒子以初速度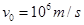 从磁场边界上直径ab的一端a射入磁场,已知该粒子的比荷
从磁场边界上直径ab的一端a射入磁场,已知该粒子的比荷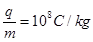 ,不计粒子重力.
,不计粒子重力.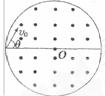
(1)求粒子在磁场中做匀速圆周运动的半径;
(2)若要使粒子飞离磁场时有最大偏转角,求入射时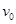 与ab的夹角
与ab的夹角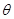 及粒子的最大偏转角.
及粒子的最大偏转角.
【答案解析】(1)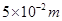 (2)
(2)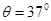 最大偏转角
最大偏转角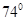
(1)粒子射入磁场后,由于不计重力,所以洛伦兹力提供圆周运动需要的向心力,根据牛顿第二定律有.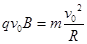
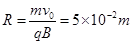
(2)粒子在圆形磁场区域运动轨迹为一段半径R=5cm的圆弧,半径一定要使偏转角最大,就要求这段圆弧对应的弦最长,即为图形区域的直径,
粒子运动轨迹的圆心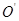 在ab弦的中垂线上,如图所示.由几何关系可知
在ab弦的中垂线上,如图所示.由几何关系可知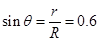
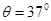
最大偏转角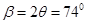
12 .
如图所示,水平放置的两平行金属板间存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度为B1,方向与纸面垂直,电场的场强E=2.0×105V/m,方向竖直向下,PQ为板间中线.紧靠平行板右侧边缘建立平面直角坐标系xOy,在第一象限内,存在着以AO为理想边界的两个匀强磁场区域,方向如图所示,磁感应强度B2=B3=0.6T,AO和y轴间的夹角θ=30°.一束带负电的粒子,质量不同,带电量q=2.5×10-8C,以v=5×105m/s的水平速度从P点射入板间,沿PQ做直线运动,穿出平行板区域后从y轴上坐标为(0,0.3m)的Q点垂直于y轴射入磁场区域.(粒子的重力不计)
(1)求磁感应强度B1的大小和方向;
(2)若粒子不能穿过AO边界,试确定其质量m应满足的条件;
(3)若m=9.0×10-15kg,求粒子从Q点进入磁场区域开始至第n次通过AO边界时的位置到原点O的距离和该过程经历的时间.(结果可保留π)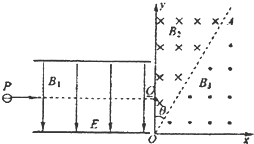
【答案解析】(1)带电粒子在板间做直线运动,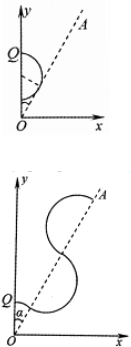
有qvB1=qE,解得:B1=
=0.4T,方向垂直于纸面向里;E v
(2)如图所示,当粒子恰好与AO边界相切时,设其轨道半径为R,
粒子质量为m0,则由几何关系可得:R+
=R sinθ
;R=. OQ
=0.1m
. OQ 3
由牛顿第二定律得:qvB2=m0
,v2 R
解得:m0=3×10-15kg
所以m≤3×10-15kg(或m<3×10-15kg)
(3)设质量m=9.0×10-15kg的粒子做匀速圆周运动的半径为r,
由牛顿第二定律得:qvB2=m
,解得:r=0.3m;v2 r
即坐标原点O为轨迹圆的圆心,粒子第一次通过AO的速度方向与AO垂直,
故粒子运动的轨迹如图所示,
设粒子第n次通过AO边界的点为An,
则
=(2n-1)r=(0.6n-0.3)m(n=1,2,3…).
AnO
带电粒子在磁场中运动的周期为T=
,2πm qB2
根据运动圆轨迹的圆心角,可得粒子第n次通过AO边界的时间为t=
+(n-1)T 12
T,1 2
t=(6n-5)π×10-7s(n=1,2,3…)
答:(1)B1为0.4T,方向向里;
(2)若粒子不能穿过AO边界,其质量m应满足的条件m≤3×10-15kg(或m<3×10-15kg);
(3)粒子从Q点进入磁场区域开始至第n次通过AO边界时的位置到原点O的距离为(0.6n-0.3)m (n=1,2,3…),该过程经历的时间(6n-5)π×10-7s (n=1,2,3…).
13 .
电子质量为m、电量为e,从坐标原点O处沿xOy平面射入第一象限(包括x轴、y轴),射入时速度方向不同,速度大小均为v0,如图所示.现在某一区域加方向向外且垂直于xOy平面的匀强磁场,并保证粒子均从O点进入磁场,磁感应强度为B,若这些电子穿过磁场后都能垂直射到荧光屏MN上,荧光屏与y轴平行,求:
(1)荧光屏上光斑的长度;
(2)所加磁场范围的最小面积.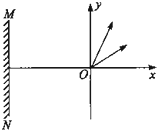
【答案解析】(1)要求光斑的长度,只要找到两个边界点即可,电子运动轨迹如图所示: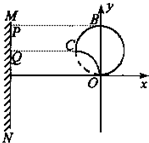
初速度沿x轴正方向的电子,沿弧OB运动到P;初速度沿y轴正方向的电子,沿弧OC运动到Q.
设粒子在磁场中运动的半径为R,由牛顿第二定律得:ev0B=m
,
v
20
R
解得:R=
,mv0
eB
由图示可知:PQ=R=
;mv0
eB
(2)沿任一方向射入第一象限的电子经磁场偏转后都能垂直打到荧光屏MN上,需加最小面积的磁场的边界是以(0,R)为圆心,半径为R的圆的一部分,如图中实线所示.
所以磁场范围的最小面积为:
S=
πR2+R2-3 4
πR2=(1 4
+1)(π 2
)2.mv0
eB
答:(1)荧光屏上光斑的长度为
;mv0
eB
(2)所加磁场范围的最小面积为(
+1)(π 2
)2.mv0
eB
14 .
如图所示,MN为两平行金属板,O、O为两金属板中心处正对的两个小孔,N板的右侧空间有磁感应强度大小均为B且方向相反的两匀强磁场区,图中N板与虚线CD、PQ为两磁场边界线,三条界线平行,两磁场区域的宽度分别为d和3d,沿边界线方向磁场区域足够大.在两金属板上加上大小可调节的直流电压,质量为m、电量为-q的带电粒子(重力不计);从O点由静止释放,经过MN板间的电场加速后,从O'沿垂直于磁场方向射入磁场,若粒子能穿过CD界并进入CD右侧磁场但不能穿过PQ界,最终打到N板而结束运动,试求:
(1)粒子要能穿过CD界并进入CD右侧磁场,MN板间的电压至少要大于多少;
(2)粒子不穿过PQ界,粒子从O射入磁场所允许的最大速率;
(3)最大速率射入磁场的粒子在磁场中运动的总时间.
【答案解析】(1)设MN间电压为U0时,若粒子在CD左侧磁场中运动的圆弧与CD界相切,如图甲,
粒子经电场加速:qU0=
mv021 2 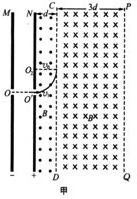
在磁场中运动的圆周半径:r0=d
qBv0=m
v02 r0
由上述得:U0=
qB2d2
2m
粒子要穿过C界,电压应大于:
.qB2d2
2m
(2)设粒子射入磁场速度为v时,粒子在CD左侧轨迹圆心为O1,右侧轨迹圆心为O2且圆弧与PQ相切,恰好不射出PQ界,
如图乙,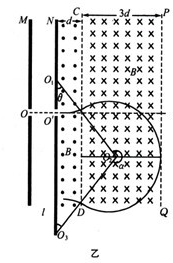
有:左右两圆周半径相同,均为r=2d
qBv=
mv2
r
得:v=
2qBd m
(3)由图得圆弧圆心角为θ=
,α=π 6
4π 3
粒子圆周运动周期:T=
=2πr v
2πm qB
粒子经过三段圆弧运动时间分别为:
t1=t3=
Tθ 2π
t2=
Tα 2π
在磁场中运动总时间:t=t1+t2+t3=
5πm 3qB
答:(1)粒子要能穿过CD界并进入CD右侧磁场,MN板间的电压至少要大于:
;qB2d2
2m
(2)粒子不穿过PQ界,粒子从O射入磁场所允许的最大速率为
;2qBd m
(3)最大速率射入磁场的粒子在磁场中运动的总时间为
.5πm 3qB
15 .
如图甲所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进 入该区域,不计重力。
入该区域,不计重力。
(1)已知粒子从外圆上以速度v1射出,求粒子在A点的初速度v0的大小。
(2)若撤去电场,如图乙,已知粒子从OA延长线与外圆的交点C以速度v2射出,方向与OA 延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间。
延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间。
(3)在图乙中,若粒子从A点进入磁场,速度大小为v3,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?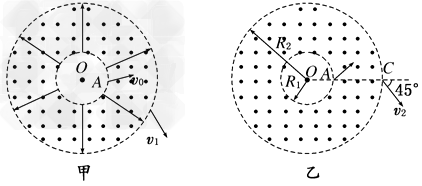
【答案解析】(1)粒子从A点进入后到由外边界射出过程,由动能定理得
qU=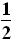 mv12-
mv12-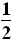 mv02①
mv02①
解得v0=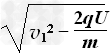 ②
②
(2)撤去电场后,作出粒子的运动轨迹如图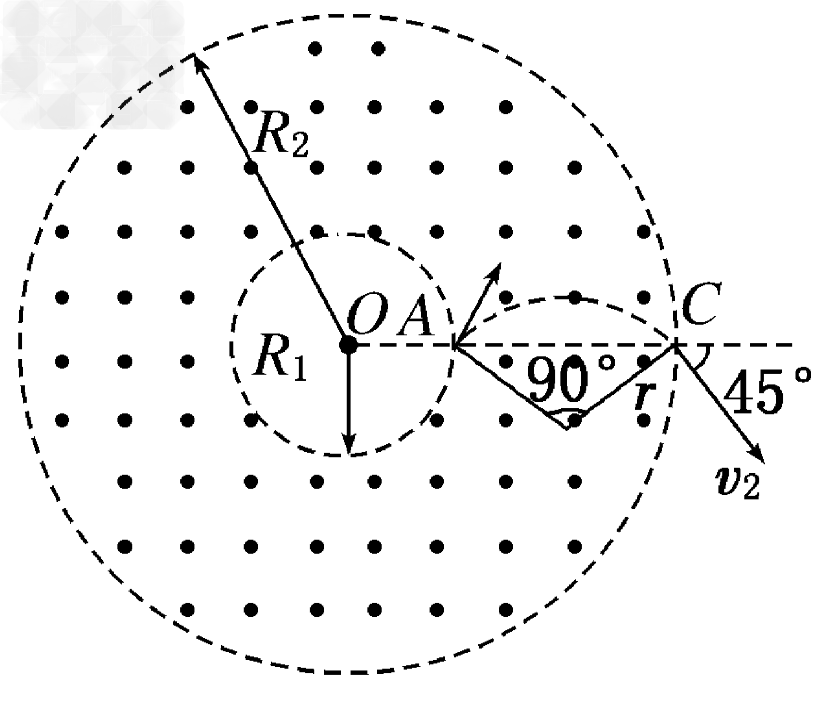
设粒子运动的轨道半径为r
由牛顿第二定律
qBv2=m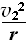 ③
③
由几何关系可知,粒子运动的圆心角为90 °,则
2r2=(R2-R1)2得r=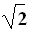 R0④
R0④
联立③④得B=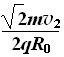 ⑤
⑤
匀速圆周运动周期T=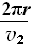 ⑥
⑥
粒子在磁场中运动时间t=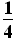 T⑦
T⑦
联立④⑥⑦,得t=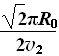 ⑧
⑧
(3)要使粒子一定能够从外圆射出,粒子刚好与两边界相切,轨迹图如图所示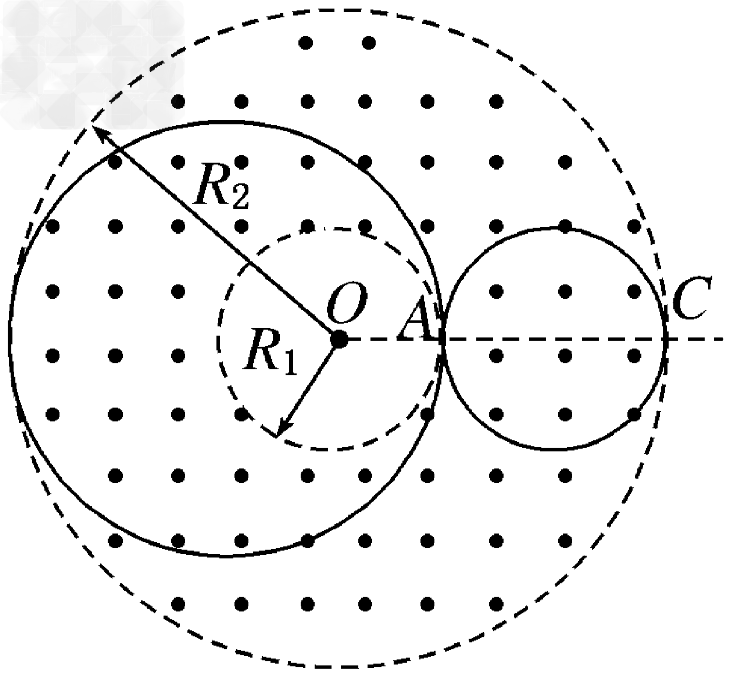
分两种情况:
第Ⅰ种情况:由几何关系可知粒子运动的轨道半径
r1=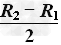 =R0⑨
=R0⑨
设此过程的磁感应强度为B1,由牛顿第二定律
qB1v3=m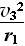 ⑩
⑩
联立⑨⑩得,B1=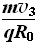
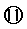
第Ⅱ种情况:由几何关系可知粒子运动轨道半径
r2=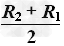 =2R0
=2R0
设此过程的磁感应强度为B2,则B2=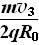
综合Ⅰ、Ⅱ可知磁感应强度应小于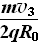
16 .
如图所示,在y轴的右侧存在磁感应强度为B的方向垂直纸面向外的匀强磁场,在x轴的上方有一平行板式加速电场。有一薄绝缘板放置在y轴处,且与纸面垂直。现有一质量为m、电荷量为q的粒子由静止经过加速电压为U的电场加速,然后以垂直于板的方向沿直线从A处穿过绝缘板,而后从x轴上的D处以与x轴负向夹角为30°的方向进入第四象限,若在此时再施加一个电场可以使粒子沿直线到达y轴上的C点(C点在图上未标出)。已知OD长为l,不计粒子的重力。求:
(1)粒子射入绝缘板之前的速度;
(2)粒子经过绝缘板时损失了多少动能;
(3)所加电场的电场强度和带电粒子在y周的右侧运行的总时间。 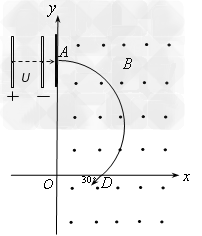
【答案解析】(1)粒子在电场中加速由动能定理可知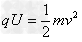
解得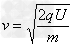
(2)粒子在磁场中作圆周运动轨迹如图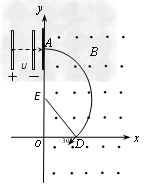
由几何关系可得轨道半径为2l
由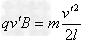
解得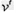 =
=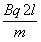
由动能定理得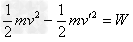
代入数据解得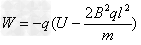
所以损失动能为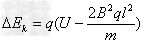
或者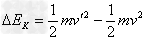 ,带入结果得
,带入结果得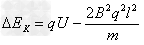
(3)粒子若作直线运动则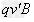 =Eq
=Eq
代入数据解得E=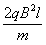 ,方向与x轴正向斜向下成60°角
,方向与x轴正向斜向下成60°角
粒子在第一象限作匀速圆周运动的时间t1=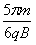
粒子在第四象限做匀速直线运动时间t2=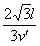 =
=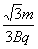
粒子x轴右侧运行的总时间t=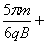
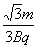 =
=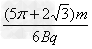
17 .
如图所示,在光滑绝缘水平桌面内放置一长为L、内壁光滑的薄壁绝缘管,在管的a端放置一个直径比管直径略小的小球,小球带电荷量为-q、质量为m。管右边的空间存在着垂直于水平桌面向上的匀强磁场,磁感应强度为B。磁场的左边界与细管平行,右边界足够远。管带着小球以水平速度v0垂直于左边界进入场中向右运动,由于水平外力F的作用,管匀速进入场中运动,一段时间后小球从管b端滑出并能在水平桌面内运动,最后从左边界飞离磁场。运动过程中小球的电荷量保持不变,不计一切阻力,求:
(1)小球从管b端滑出时速度的大小;
(2)从管进入场至小球从b端滑出的过程中,外力F所做的功;
(3)从细管进入磁场至小球离开磁场的过程中小球的最大位移。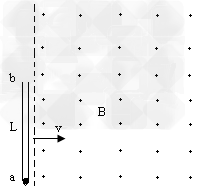
【答案解析】(1)小球在管中和管一起向右运动,受到指向管口的洛仑兹力的作用,产生的加速度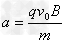
小球运动到管口时的速度(相对于管)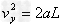
因此小球从管中出来时的速度为(相对于磁场)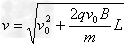
(2)管匀速运动,故小球在管中运动时,F是变力,随管的位移而均匀增大,所以F做的功可由动能定理得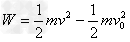
得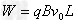
(3)设小球在磁场中运动的半径为R,根据题意分析,运动的情况如图示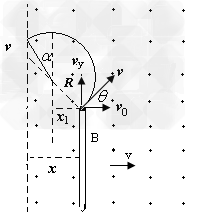
小球在管中的运动时间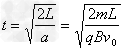
小球向右运动的位移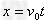
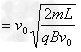
又因洛仑兹力提供带电粒子做圆周运动的向心力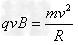
由图可知几何关系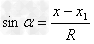 和
和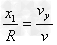
得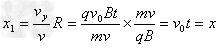 ,即
,即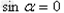 ,
,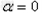
即小球飞离磁场时的速度与左侧的边界垂直,运动的最大位移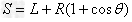
其中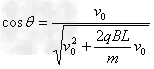 ,
,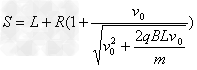
18 .
如图所示,虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域,电场强度的大小为E,方向向下,磁感应强度为B,方向垂直纸面向外,PQ为其分界线,现有一群质量为m,电荷量为-e的电子(重力不计)从PQ中点与PQ成30°角以不同的初速射入磁场,求:
(1)能从PQ边离开磁场的电子在磁场运动的时间.
(2)若要电子在磁场运动时间最长,其初速v应满足的条件?
(3)若电子在满足(2)中的条件下且以最大速度进入磁场,最终从电场aP边界飞出虚线框所具有的动能Ek。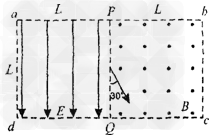
【答案解析】(1)由洛仑兹力充当向心力:eBv=m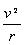 ①
①
电子在磁场中运动的周期:T=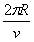 ②
②
①②解得:T=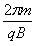
能从PQ边进入电场(如图).粒子在匀强磁场中运动时间为t,由图知t=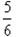 T ③
T ③
解得:t=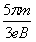
(2)当电子轨迹与Pb边相切时,有满足条件的最大速度v,由几何关系知其轨道半径r满足
r+rsin30°=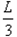 ④ r=
④ r=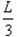
洛仑兹力充当向心力:eBv=m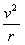
①④解得v=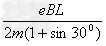 =
=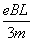
因此,当v≤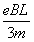 时,电子有磁场运动有最长时间
时,电子有磁场运动有最长时间
(结果表示为v<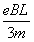 ,0<v<
,0<v<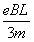 ,0<v≤
,0<v≤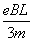 均正确)
均正确)
(3)以最大速度v进入电场,且从aP边飞出时电子有最大动能EKM,由动能定理:
eE(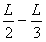 )=Ekm-
)=Ekm-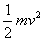 ⑥
⑥
解得Ekm=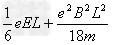
19 .
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角。紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27 kg,电荷量q = 3.2×10-19 C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°= 0.8)求:
(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子穿出金箔进入电场(速度方向与离开磁场的方向一致),在电场中运动通过N点,SN⊥ab且SN = 40cm,则此α粒子从金箔上穿出时,损失的动能△EK为多少?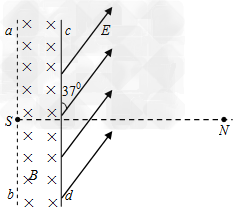
【答案解析】(1)α粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即: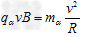
则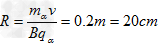
(2)设cd中心为O,则: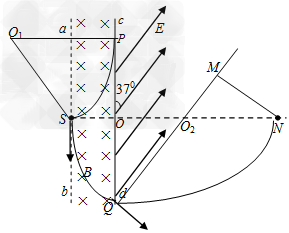
向c端偏转的α粒子,当圆周轨迹与cd相切时偏离O最远,设切点为P,对应圆心O1,如图所示,则由几何关系得: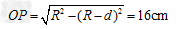
向d端偏转的α粒子,当沿sb方向射入时,偏离O最远,设此时圆周轨迹与cd交于Q点,对应圆心O2,如图所示,则由几何关系得: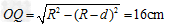
故金箔cd被α粒子射中区域的长度
(3)设从Q点穿出的α粒子的速度为v',因半径O2Q与场强E的方向间的夹角θ,有:tanθ=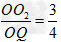 ,故穿出的α粒子在电场中做类平抛运动,轨迹如上图所示
,故穿出的α粒子在电场中做类平抛运动,轨迹如上图所示
沿速度v'方向做匀速直线运动, 位移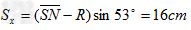
沿场强E方向做匀加速直线运动,位移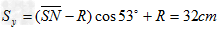
则由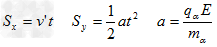
得: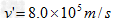
故此α粒子从金箔上穿出时,损失的动能为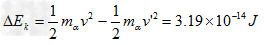
20 .
据有关资料介绍,受控核聚变装置中有极高温度,因而带电粒子没有通常意义上的“容器”可装,而是由磁场约束带电粒子运动使之束缚在某个区域内.现按下面的简化条件来讨论这个问题:如图所示是一个截面为内径R1=0.6m 外径R2=1.2m的环状区域,区域内有垂直于截面向里的匀强磁场.已知氦核的比荷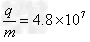 C/kg,磁场的磁感应强度B=0.4T,不计带电粒子的重力.
C/kg,磁场的磁感应强度B=0.4T,不计带电粒子的重力.
(1)实践证明,氦核在磁场区域内沿垂直于磁场方向运动速度v的大小与它在磁场运动的轨道半径r有关,试导出v与r的关系式.
(2)若氦核沿磁场区域的半径方向平行于截面从A点射入磁场,画出氦核在磁场中运动而不穿出外边界的最大圆轨道示意图,并求出此圆轨道的半径.
(3)若氦核在平行于截面从A点沿各个方向射入磁场都不能穿出磁场外边界,求氦核的最大速度.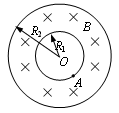
【答案解析】(1)氦核在磁场区域内沿垂直于磁场方向运动时,由洛仑兹力提供做圆周运动的向心力,有: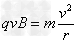 ,得:
,得: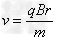
(2)当氦核垂直于内圆从A点射入磁场,并且与外圆相切时轨道半径最大,其运动轨迹如图a所示.三角形OO'A为直角三角形,设此圆轨道的半径为rm,由勾股定理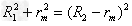 得:
得: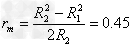 m
m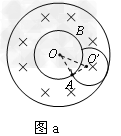
(3)当氦核以速度vm沿与内圆相切方向射入磁场且与外圆相切时,则氦核在平行于截面从A点沿各个方向射入磁场都不能穿出磁场外边界,如图b所示.设此时轨道半径为r',由几何关系,有: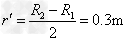 ,由
,由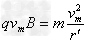 得:
得: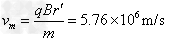
21 .
如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里。电量为q、质量为m的带正电的粒子从磁场边缘A点沿圆的半径AO方向射入磁场,离开磁场时速度方向偏转了60°角。试确定:
(1)粒子做圆周运动的半径。
(2)粒子的入射速度。
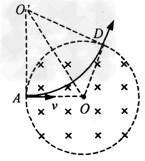
(3)若保持粒子的速率不变,从A点入射时速度的方向顺时针转过60°角,粒子在磁场中运动的时间。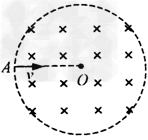
【答案解析】(1)设带电粒子在匀强磁场中做匀速圆周运动半径为R,如图所示,∠OO'A = 30°,由图可知,圆运动的半径R= O'A = 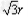
(2)根据牛顿运动定律, 有:Bqv = m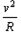
有:R = 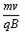
故粒子的入射速度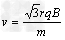
(3)当带电粒子入射方向转过60°角,如图所示,在△OAO1中,OA= r,O1A= 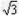 r,∠O1AO=30°,由几何关系可得,O1O=r,∠AO1E=60°
r,∠O1AO=30°,由几何关系可得,O1O=r,∠AO1E=60°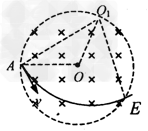
设带电粒子在磁场中运动所用时间为t,由: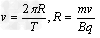
有:T = 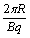
解出:t = 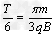
22 .
如图,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.60T,磁场内有一块平面感光板ab,板面与磁场方向平行,在距ab的距离l=16cm处,有一个点状的α放射源S,它向各个方向发射α粒子,α粒子的速度都是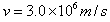 ,已知α粒子的电荷与质量之比
,已知α粒子的电荷与质量之比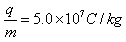 ,现只考虑在图纸平面中运动的α粒子,求ab上被α粒子打中的区域的长度。
,现只考虑在图纸平面中运动的α粒子,求ab上被α粒子打中的区域的长度。 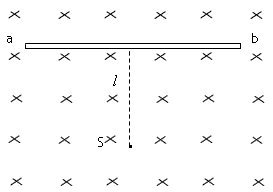
【答案解析】α粒子带正电,故在磁场中沿逆时针方向做匀速圆周运动,用R表示轨道半径,有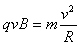 ①
①
由此得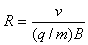
代入数值得R=10cm
可见,2R>l>R
因朝不同方向发射的α粒子的圆轨迹都过S,由此可知,某一圆轨迹在图中N左侧与ab相切,则此切点P1就是α粒子能打中的左侧最远点。为定出P1点的位置,可作平行于ab的直线cd,cd到ab的距离为R,以S为圆心,R为半径,作弧交cd于Q点,过Q作ab的垂线,它与ab的交点即为P1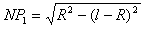 ②
② 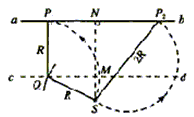
再考虑N的右侧,任何α粒子在运动中离S的距离不可能超过2R,以2R为半径、S为圆心作圆,交ab于N右侧的P2点,此即右侧能打到的最远点
由图中几何关系得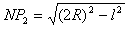 ③
③
所求长度为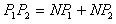 ④
④
代入数值得P1P2=20cm ⑤
23 .
如图所示,在真空中半径r=3.0×10-2 m的圆形区域内,有磁感应强度B=0.2T、方向垂直于纸面向里的匀强磁场。一批带正电的粒子以初速度v0=1.0×106 m/s从磁场边界上的一点a向着纸面内的各个方向射入磁场,该粒子的比荷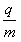 =1.0×108 C/kg,不计粒子重力。
=1.0×108 C/kg,不计粒子重力。
(1)求粒子在磁场中运动的最长时间;
(2)若射入磁场时的速度改为v0=3.0×105 m/s,其他条件不变,试用斜线在图中描绘出该粒子可能出现的区域。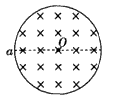
【答案解析】粒子在磁场中运动的圆弧所对应的圆心角最大时,粒子在磁场中运动的时间最长,以此求出最长时间。根据粒子由a点向着各个方向射入磁场,画出它们的轨迹示意图,确定粒子在磁场中可能出现的区域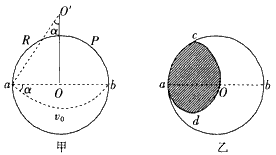
(1)粒子以速度v0=1.0×106 m/s射入磁场,在洛伦兹力作用下做匀速圆周运动,则有: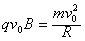
解得:R=5.0×10-2 m
其最长时间tm=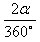 ×T
×T 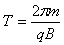
由三角形可知sinα=0.6,得α=37°
解得:tm=6.5×10-8 s
(2)当v0=3.0×105 m/s时,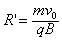 =1.5×10-2 m=
=1.5×10-2 m=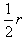
由于粒子逆时针方向做圆周运动,因此粒子能到达的位置边缘是以aO为直径的半圆弧adO和以a为圆心、r为半径的圆弧Oc
即粒子在磁场中可能出现的区域为图乙中画斜线的部分
24 .
电子质量为m,电荷量为e,从坐标原点O处沿xOy平面射入第一象限,射入时速度方向不同,速度大小均为v0,如图所示。现在某一区域加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度为B,若这些电子穿过磁场后都能垂直射到荧光屏MN上,荧光屏与y轴平行,求:
(1)电子从y轴穿过的范围;
(2)荧光屏上光斑的长度;
(3)所加磁场范围的最小面积。 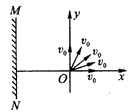
【答案解析】(1)设磁场中运动的半径为R ,牛顿第二定律得: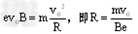
电子从y轴穿过的范围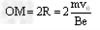
(2)如图所示,求光斑长度,关键是找到两个边界点,初速度方向沿x轴正方向的电子,沿弧OB运动到P;初速度方向沿y轴正方向的电子,沿弧OC运动到Q
电子在磁场中的半径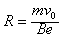
由图可知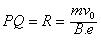
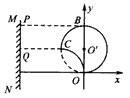
(3)沿任一方向射入第一象限的电子经电场偏转后都能垂直打到荧光屏MN上,所加最小面积的磁场的边界是以O'(0,R)为圆心,R为半径的圆的一部分,如图中实线所示,所以磁场范围的最小面积为