首页 请复制到word或wps中编辑使用(ctrl+c,ctrl+v),vip用户页面底部可看到答案解析 公式上下对齐方法
锐角三角函数
一.单选题
(共 2 小题)
1 .
如图，长4m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后的楼梯AC的长为( )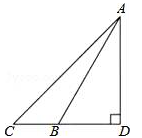
A、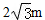
B、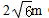
C、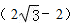
D、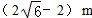
【答案解析】B
【分析】先在Rt△ABD中利用正弦的定义计算出AD，然后在Rt△ACD中利用正弦的定义计算AC即可．
【解答】解：在Rt△ABD中，∵sin∠ABD=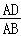
，
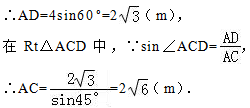
故选B．
2 .
如图是一楼与二楼之间的手扶电梯示意图，AB、CD分别表示一楼、二楼地面的水平线，∠ABC=140°，BC的长是8米，则乘电梯从点B到点C上升的高度h可以表示为( )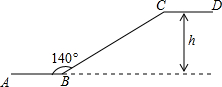
A、8sin40°米
B、8cos40°米
C、8tan40°米
D、8tan50°米
【答案解析】A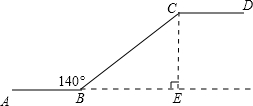
解：过C作CE⊥AB，交AB的延长线于E；
在Rt△CBE中，∠CBE=180°-∠CBA=40°；
已知BC=8m，则CE=BC•sin40°，即h=8sin40°米．
故选：A．
二.填空题
(共 1 小题)
1 .
如图，某山坡的坡面AB=200米，坡角∠BAC=30°，则该山坡的高BC的长为 米．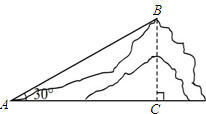
【答案解析】100
解：由题意得，∠BCA=90°，∠BAC=30°，AB=200米，
故可得BC=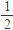
AB=100米．
故答案为：100．
三.解答题
(共 3 小题)
1 .
如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．
(1)求AB段山坡的高度EF；
(2)求山峰的高度CF．(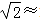
1.414，CF结果精确到米)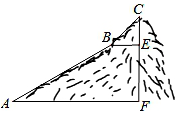
【答案解析】解：(1)作BH⊥AF于H，如图，
在Rt△ABF中，∵sin∠BAH=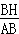
，
∴BH=800•sin30°=400，
∴EF=BH=400m；
(2)在Rt△CBE中，∵sin∠CBE=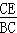
，
∴CE=200•sin45°=100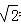
≈141.4，
∴CF=CE+EF=141.4+400≈541(m)．
答：AB段山坡高度为400米，山CF的高度约为541米．
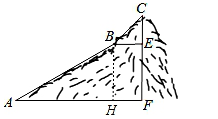
【分析】(1)作BH⊥AF于H，如图，在Rt△ABF中根据正弦的定义可计算出BH的长，从而得到EF的长；
(2)先在Rt△CBE中利用∠CBE的正弦计算出CE，然后计算CE和EF的和即可．
【解答】解：(1)作BH⊥AF于H，如图，
在Rt△ABF中，∵sin∠BAH=，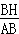
∴BH=800•sin30°=400，
∴EF=BH=400m；
(2)在Rt△CBE中，∵sin∠CBE=，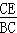
∴CE=200•sin45°=100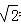≈141.4，
∴CF=CE+EF=141.4+400≈541(m)．
答：AB段山坡高度为400米，山CF的高度约为541米．
2 .
如图，防洪大堤的横截面是梯形ABCD，其中AD∥BC，α=60°，汛期来临前对其进行了加固，改造后的背水面坡角β=45°．若原坡长AB=20m，求改造后的坡长AE．(结果保留根号)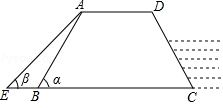
【答案解析】解：过点A作AF⊥BC于点F，
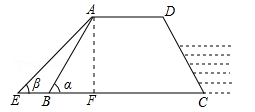
在Rt△ABF中，∠ABF=∠α=60°，
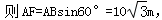
在Rt△AEF中，∠E=∠β=45°，
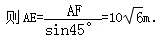
答：改造后的坡长AE为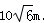
分析：过点A作AF⊥BC于点F，在Rt△ABF中求出AF，然后在Rt△AEF中求出AE即可
解：过点A作AF⊥BC于点F，
在Rt△ABF中，∠ABF=∠α=60°，
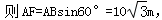
在Rt△AEF中，∠E=∠β=45°，
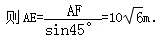
答：改造后的坡长AE为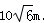
3 .
如图，
是某市一座人行天桥的示意图，天桥离地面的高BC是10米，坡面10米处有一建筑物HQ，为了方便使行人推车过天桥，市政府部门决定降低坡度，使新坡面DC的倾斜角∠BDC=30°，若新坡面下D处与建筑物之间需留下至少3米宽的人行道，问该建筑物是否需要拆除(计算最后结果保留一位小数)．(参考数据：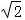
=1.414，
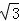=1.732)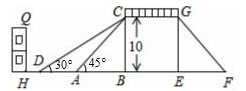
【答案解析】解：由题意得，AH=10米，BC=10米，
在Rt△ABC中，∠CAB=45°，
∴AB=BC=10，
在Rt△DBC中，∠CDB=30°，
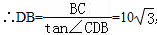
∴DH=AH﹣AD=AH﹣(DB﹣AB)=10﹣10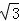+10=20﹣10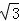≈2.7(米)，
∵2.7米＜3米，
∴该建筑物需要拆除．
【分析】根据正切的定义分别求出AB、DB的长，结合图形求出DH，比较即可．
【解答】解：由题意得，AH=10米，BC=10米，
在Rt△ABC中，∠CAB=45°，
∴AB=BC=10，
在Rt△DBC中，∠CDB=30°，
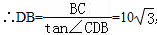
∴DH=AH﹣AD=AH﹣(DB﹣AB)=10﹣10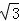+10=20﹣10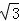≈2.7(米)，
∵2.7米＜3米，
∴该建筑物需要拆除．