作者 : ixvy 期中 · 高一上学期
收藏试卷 下载试卷 派生 全部添加至试题篮
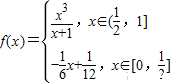 ,函数
,函数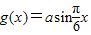 -a+1(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
-a+1(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
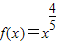 ,若0<x1<x2,则
,若0<x1<x2,则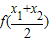 ,
,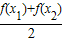 大小关系是 .
大小关系是 .
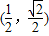 ,则f(x)在(0,+∞)单调递 .
,则f(x)在(0,+∞)单调递 .
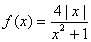 的四个命题:
的四个命题: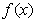 的图像关于
的图像关于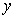 轴对称;
轴对称;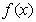 在区间
在区间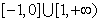 上单调递减;
上单调递减;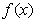 在
在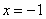 处取得极小值,在
处取得极小值,在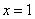 处取得极大值;
处取得极大值;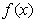 的有最大值,无最小值;
的有最大值,无最小值;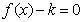 至少有三个不同的实根,则实数
至少有三个不同的实根,则实数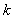 的取值范围是
的取值范围是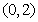 。
。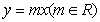 与函数
与函数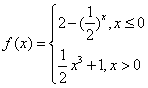 的图象恰有三个不同的公共点,则实数m的取值范围是 .
的图象恰有三个不同的公共点,则实数m的取值范围是 .
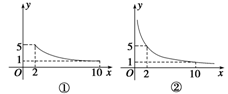
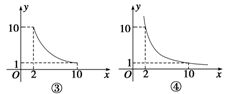
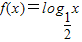 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称,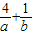 的最大值为
的最大值为 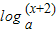 =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
 ,给出下列四个命题:
,给出下列四个命题: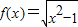 ,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是 .
,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是 .


 ,a∈R.若对于任意的x∈N,f (x)≥4恒成立,则a的取值范围是 .
,a∈R.若对于任意的x∈N,f (x)≥4恒成立,则a的取值范围是 .
 ,其中x∈[0,2],若4∈M,2∈N,则a的范围是 .
,其中x∈[0,2],若4∈M,2∈N,则a的范围是 .
 ,③f(x)=
,③f(x)=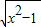 ,④f(x)=x2,⑤f(x)=e-x,
,④f(x)=x2,⑤f(x)=e-x,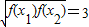 成立的函数序号是 .
成立的函数序号是 .
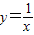 ; ②y=2x;③y=sinx;④y=1nx
; ②y=2x;③y=sinx;④y=1nx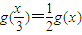 ;
;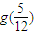 = .
= .
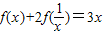 ,则函数g(x)=f(2x)在(0,1)上有唯一零点;
,则函数g(x)=f(2x)在(0,1)上有唯一零点;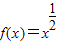 的定义域中任意的x1、x2(x1≠x2)必有
的定义域中任意的x1、x2(x1≠x2)必有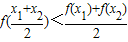 ;
;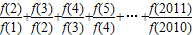 = .
= .
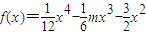 .
.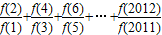 = .
= .
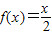 ,则
,则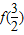 = .
= .
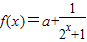 是奇函数,则a= .
是奇函数,则a= .
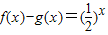 ,则f(1)g(0)g(-2)从小到大的顺序为 .
,则f(1)g(0)g(-2)从小到大的顺序为 .
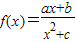 的图象如下,则a,b,c的大小顺序为 .
的图象如下,则a,b,c的大小顺序为 .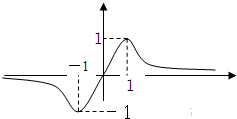
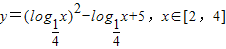 的值域为 .
的值域为 .
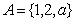 与集合
与集合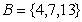 ,若
,若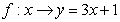 是从
是从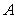 到
到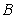 的映射则
的映射则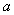 的值为_________________.
的值为_________________.
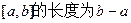 ,区间
,区间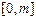 在映射
在映射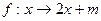 所得的对应区间为
所得的对应区间为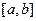 ,若区间
,若区间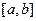 的长度比区间
的长度比区间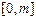 的长度大5,则m= _ .
的长度大5,则m= _ .
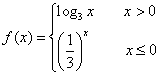 ,则不等式
,则不等式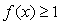 的解集为_____________.
的解集为_____________.
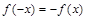 ”的分段函数
”的分段函数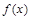 叫做“对偶函数”,已知函数
叫做“对偶函数”,已知函数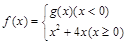 是“对偶函数”,则(1)
是“对偶函数”,则(1)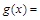 ;
;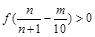 对任意正整数
对任意正整数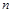 都成立,实数
都成立,实数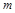 的取值范围为 .
的取值范围为 .
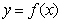 满足:
满足: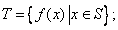 (ii)对任意
(ii)对任意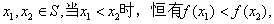
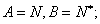
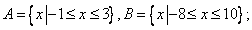
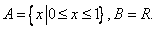
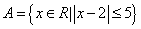 中最小整数位 .
中最小整数位 .
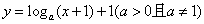 的图象必经过定点(0,1);
的图象必经过定点(0,1); :
: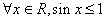 ,则
,则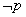 :
: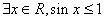 ;
;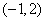 且与直线
且与直线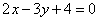 垂直的直线方程为
垂直的直线方程为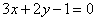 ;
;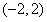 上随机抽取一个数
上随机抽取一个数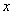 ,则
,则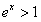 的概率为
的概率为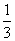 。
。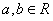 ,集合
,集合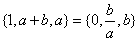 ,则
,则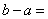 .
.
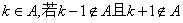 ,则k是A的一个“孤立元”,给定
,则k是A的一个“孤立元”,给定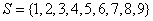 ,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。
,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。
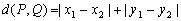 为两点
为两点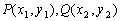 之间的“折线距离”,在这个定义下,给出下列命题:
之间的“折线距离”,在这个定义下,给出下列命题: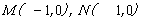 两点的“折线距离”之和为4的点的集合是面积为6的六边形;
两点的“折线距离”之和为4的点的集合是面积为6的六边形;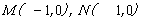 两点的“折线距离”差的绝对值为1的点的集合是两条平行线;
两点的“折线距离”差的绝对值为1的点的集合是两条平行线;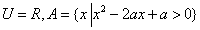 ,如果
,如果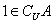 ,那么
,那么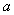 的取值范围是_____.
的取值范围是_____.