二、 填空题 (共 18 小题)
收 起
已知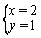 是方程2x+ky=3的解,则k=( )。
是方程2x+ky=3的解,则k=( )。
已知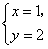 是方程ax-3y=5的一个解,则a=( )
是方程ax-3y=5的一个解,则a=( )
已知二元一次方程4x-5y=20,用含x的代数式表示y,则y=( )
已知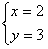 是方程5x-( k-1)y-7 = 0的一个解,则k =( )
是方程5x-( k-1)y-7 = 0的一个解,则k =( )
麦迪在一次比赛中22投14中得28分,除了3个三分球全中外,他还投中了( )两分球和( )个罚球.
一批旅客决定分乘几辆大汽车,并且要使每辆车有相同的人数.起先,每辆车乘坐22人,发现有一人坐不上车.若是开走一辆空车,那么所有的旅客刚好平均分乘余下的汽车.已知每辆车的载客量不能多于32人,则原有______辆汽车,这批旅客有______人.
某校组织部分少先队员去看文艺表演,老师派队长先去购票,已知甲等票每张10元,乙等票每张8元,队长带去450元,买了45张票,找回50元, 则队长甲等票买了( )张。
某次数学竞赛中,只有20个选择题,对每个选择题做对得8分,做错扣5分,不做记零分,已知A在这次考试中的得分是13的整数倍,则A在这次考试中没有做的题的个数为______.
甲种物品每个4千克,乙种物品每个7千克,现有甲种物品x个,乙种物品y个,共76千克:(1)列出关于x、y的二元一次方程______;(2)若x=12,则y=______;(3)若有乙种物品8个,则甲种物品有______个.
书店有单价为10分、15分、25分、40分的四种贺年卡,小华花了几张一元的钱正好买了30张贺年卡,其中的两种各买了5张,另两种各买了10张,那么小华买贺年卡共花了______元钱.
小张带了50元钱去买橡皮与钢笔.橡皮每块3元,钢笔每支11元.小张买了所需物品刚好用光所有钱,则他买了 支钢笔.
某商人经营甲、乙两种商品,每件甲种商品的利润率为40%,每件乙种商品的利润率为60%,当售出的乙种商品的件数比甲种商品的件数多50%时,这个商人得到的总利润率是50%;当售出的乙种商品的件数比甲种商品的件数少50%时,这个商人得到的总利润率为 .
(利润率=利润÷成本)
某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位.要求租用的车辆不留空座,也不能超载.有 种租车方案.
用甲乙两种饮料按照x:y(重量比)混合配制成一种新饮料,原来两种饮料成本是:甲每300克5元,乙每300克3元.现甲成本上升10%,乙下降10%,而新饮料成本恰好保持不变,则x:y= .
小彬拿20元钱到超市买来果汁x瓶,酸奶y瓶,找回7元,已知果汁每瓶2元,酸奶每瓶3元,列出关于x、y的二元一次方程为______.
某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位.要求租用的车辆不留空座,也不能超载.有 种租车方案.
三、 解答题 (共 15 小题)
收 起
已知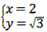 是关于x,y的二元一次方程
是关于x,y的二元一次方程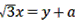 的解,求(a+1)(a-1)+7的值。
的解,求(a+1)(a-1)+7的值。
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加。为了缓解停车矛盾,某小区据顶投资15万元建造若干个停车位。建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?写出所有可能的方案。
设R为平面上以A(4,1)、B(-1,-6)、C(-3,2)三点为顶点的三角形区域(包括三角形内部及周界)。试求当(x,y)在R上变动时,函数4x-3y的极大值和极小值(须证明你的论断)。
甲、乙两车间同生产一种零件,甲车间有1人每天生产6件,其余每人每天生产11件,乙车间有1人每天生产7件,其余每人每天生产10件,已知各车间生产的零件数相等,且不少于100件又不超过200件,求甲、乙车间各有多少名工人?
某单位共有36名员工,要乘汽车外出旅游,可租用的汽车有两种,一种每辆可乘8人,另一种每辆可乘4人,要求租用的汽车不留空位,也不能超载.
(1)请你给出不同的租车方案(至少3种);
(2)若每辆8个座位的汽车的租金是每天300元,每辆4个座位的汽车的租金是每天200元,请你设计出费用最低的租车方案,并说明理由.
阳光公司决定按如图(1)给出的比例,从甲、乙、丙三个工厂共购买200件同种产品A,已知这三个工厂生产的产品A的优品率如表所示.
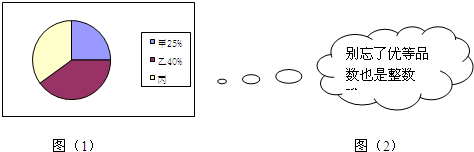
(1)阳光公司从甲厂应购买______件产品A,从乙厂应购买______件产品A,从丙厂应购买______件产品A;
(2)阳光公司所购买的200件产品A的优品率为______;
(3)你认为阳光公司能否通过调整从三个工厂所购买的产品A的比例(每个工厂的购买数均大于0),使所购买的200件产品A的优品率上升3%?若能,请问应从甲厂购买多少件产品A;若不能,请说明理由.(如图(2))
把一根lm长的金属线材,截成长为23cm和13cm的两种规格,用怎样的方案截取材料利用率最高?求出最高利用率.(利用率=×100%,截口损耗不计)
已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
一个家电维修中心有技术员工和辅助员工共15人,技术员工数是辅导员工数的2倍.家电维修中心计划对员工发放奖金共计20000元,按“技术员工个人奖金”A元和“辅导员工个人奖金”B元两种标准发放,其中A≥B≥800,并且A,B都是100的整数倍.
(1)求该家电维修中心中技术员工和辅导员工的人数;
(2)求本次奖金发放的具体方案?
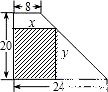
如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形(阴影部分)铁片备用,当要求截取的矩形两边长的比x:y=4:5时,矩形的面积是多少?
某县政府打算用25 000元用于为某乡福利院购买每台价格为2 000元的彩电和每台价格为1 800元的冰箱,并计划恰好全部用完此款.
(1)问原计划所购买的彩电和冰箱各多少台;
(2)由于国家出台“家电下乡”惠农政策,该县政府购买的彩电和冰箱可获得13%的财政补贴,若在不增加县政府实际负担的情况下,能否多购买两台冰箱?谈谈你的想法.
某县政府打算用25 000元用于为某乡福利院购买每台价格为2 000元的彩电和每台价格为1 800元的冰箱,并计划恰好全部用完此款.
(1)问原计划所购买的彩电和冰箱各多少台;
(2)由于国家出台“家电下乡”惠农政策,该县政府购买的彩电和冰箱可获得13%的财政补贴,若在不增加县政府实际负担的情况下,能否多购买两台冰箱?谈谈你的想法.
2011年3月10日12时58分,在云南盈江县发生5.8级地震,随后又相继发生里氏4.7级、里氏4.5级、里氏3.6级余震。灾情发生后,全国人民抗震救灾,众志成城。湖州市政府也筹集了抗震救灾物资共120吨准备运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
| 甲
| 乙
| 丙
|
汽车运载量(吨/辆)
| 5
| 8
| 10
|
汽车运费(元/辆)
| 400
| 500
| 600
|
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总车辆数为14辆,你能分别求出三种车型的车辆数吗?此时的运费又是多少元?
九年级某班组织班团活动,班委会准备买一些奖品.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件.
(1)有多少种购买方案?请列举所有可能的结果;
(2)从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率.
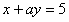 有一个解是
有一个解是 ,则
,则 的值是
的值是 

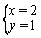 是方程2x+ky=3的解,则k=( )。
是方程2x+ky=3的解,则k=( )。 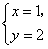 是方程ax-3y=5的一个解,则a=( )
是方程ax-3y=5的一个解,则a=( ) 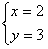 是方程5x-( k-1)y-7 = 0的一个解,则k =( )
是方程5x-( k-1)y-7 = 0的一个解,则k =( ) 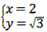 是关于x,y的二元一次方程
是关于x,y的二元一次方程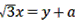 的解,求(a+1)(a-1)+7的值。
的解,求(a+1)(a-1)+7的值。 
 型车和1辆
型车和1辆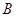 型车装满货物一次可运货10吨;用1辆
型车装满货物一次可运货10吨;用1辆 型车和2辆
型车和2辆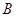 型车装满货物一次可运货11吨,某物流公司现有31吨货物,计划同时租用
型车装满货物一次可运货11吨,某物流公司现有31吨货物,计划同时租用 型车
型车 辆,
辆,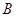 型车
型车 辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题: 型车和1辆
型车和1辆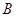 型车都装满货物一次可分别运货多少吨?
型车都装满货物一次可分别运货多少吨? 型车每辆需租金100元/次,
型车每辆需租金100元/次,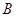 型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费. 