圆的考试
作者 : 2110
随堂 · 九年级上
收藏试卷
显示答案
下载试卷
纯净版
派生
全部添加至试题篮
一、 单选题 (共 3 小题)
收 起
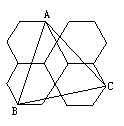
如图,四个正六边形的面积都是6,则图中△ABC的面积等于( ).
已知,正六边形的半径是 ,则这个正六边形的边长是
,则这个正六边形的边长是
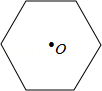
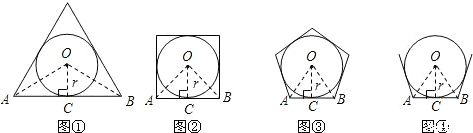
如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是【 】
二、 填空题 (共 5 小题)
收 起
半径为r的圆内接正三角形的边长为 .(结果可保留根号)
已知正六边形ABCDEF的边长为2cm,点P为正六边形内部的一个动点,则点P到这个正六边形各边的距离之和为 cm.
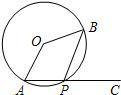
如图,圆心角∠AOB=120°,P是  |
| AB |
上任一点(不与A,B重合),点C在AP的延长线上,则∠BPC等于 ______.
(选做题)
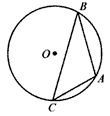
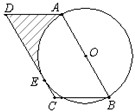
如图,点A、B、C是圆O上的点,且BC=6,∠BAC=120°,则圆O的面积等于( )。
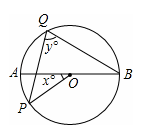
如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,则y与x的函数关系是 .
三、 解答题 (共 18 小题)
收 起
如图,已知在⊙O中,直径AB为8cm,弦AC为4 cm,∠ACB的平分线交⊙O于D,连结BC,AD.【小题1】(1)求BC的长. 【小题2】(2)求∠CAD的度数
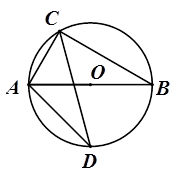
(选做题)如图,AB是圆O的直径,D,E为圆上位于AB异侧的两点,连接BD并延长至点C,使BD=DC,连接AC,AE,DE,求证:∠E=∠C。
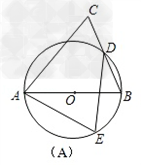
如图,⊙O的直径是AB,CD是⊙O的弦,若∠D=70°,则∠ABC等于 .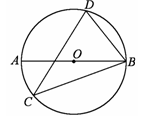
(选做题)
如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F。求证:
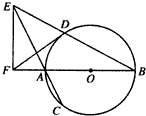
(1)∠DEA=∠DFA;
(2)AB2=BE·BD-AE·AC。
如图,AB是⊙O的直径,点C在⊙O上,AB=6,AC=5,求tanA的值.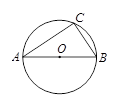
如图,在⊙O中,AB是直径,且长度为 2,劣弧 BC 的长为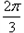 。
。
(1)求∠AOC的度数;
(2)若D为劣弧 BC上的一个动点,且AD与OC交于点E,试探求当△AEC≌△DEO时,D点的位置。
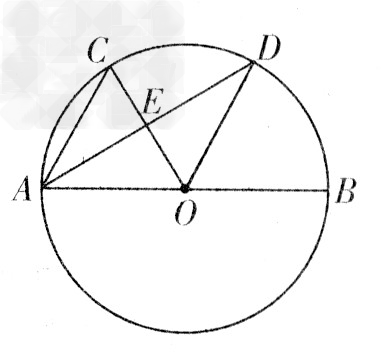
某课题小组对课本的习题进行了如下探索,请逐步思考并解答:
(1)如图1,两个大小一样的传送轮连接着一条传送带,两个传动轮中心的距离是10m,求这条传送带的长 _________
(2)改变图形的数量;如图2、将传动轮增加到3个,每个传动轮的直径是3m,每两个传动轮中心的距离是10m,求这条传送带的长 _________ ;
(3)改变动态关系,将静态问题升华为动态问题:如图3,一个半径为1cm的⊙P沿边长为2πcm的等边三角形△ABC的外沿作无滑动滚动一周,求圆心P经过的路径长?⊙P自转了多少周?
(4)拓展与应用如图4,一个半径为1cm的⊙P沿半径为3cm的⊙O外沿作无滑动滚动一周,则⊙P自转了多少周? 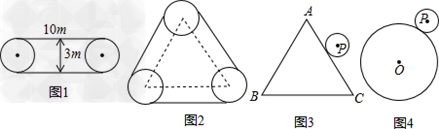
如图,点A是半圆上的一个三等分点,点B是弧AN的中点,点P是直径MN上一个动点,圆O的半径为1,
【小题1】(1)找出当AP+BP能得到最小值时,点P的位置,并证明
【小题2】(2)求出AP+BP最小值
已知:如图,在⊙O中,AB=CD.
求证:∠ABD=∠CDB
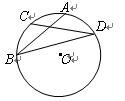
如图,已知AB是⊙O的直径,点D、E在⊙O上,且︵AD∶︵DE=3∶5, ︵BE的度数为20°,连接DE并延长交AB的延长线于C,
【小题1】求∠AOD的度数;
【小题2】判断CE与AB有什么数量关系,并说明理由
已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.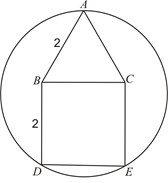
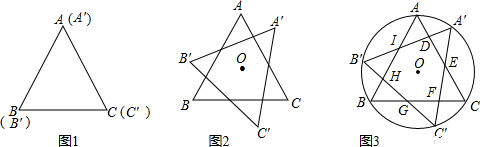
如图1,边长均为6的正△ABC和正△A′B′C′原来完全重合.如图2,现保持正△ABC不动,使正△A′B′C′绕两个正三角形的公共中心点O按顺时针方向旋转,设旋转角度为α(α>0°).(注:除第 (3)题中的第②问,其余各问只要直接给出结果即可)
(1)当α多少时,正△A′B′C′与正△ABC出现旋转过程中的第一次完全重合?
(2)当0°<α<360°时,要使正△A′B′C′与正△ABC重叠部分面积最小,α可以取哪些角度?
(3)旋转时,如图3,正△ABC和正△A′B′C′始终具有公共的外接圆⊙O.当0°<α<60°时,记正△A′B′C′与正△ABC重叠部分为六边形DEFGHI.当α在这个范围内变化时,
①求△ADI面积S相应的变化范围;
②△ADI的周长是否一定?说出你的理由.
如图,Rt△ABC中∠C=90°、∠A=30°,在AC边上取点O画圆使⊙O经过A、B两点。
(1)求证:以O为圆心,以OC为半径的圆与AB相切;
(2)下列结论正确的序号是 _________ .(少选酌情给分,多选、错均不给分)
①AO=2CO;
②AO=BC;
③延长BC交⊙O与D,则A、B、D是⊙O的三等分点;
④图中阴影面积为: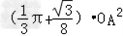 .
.
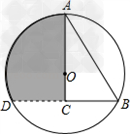
在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E。
(1)求圆心O到CD的距离;
(2)求DE的长;
(3)求由弧AE、线段AD、DE所围成的阴影部分的面积。(结果保留π和根号)

 ,则这个正六边形的边长是
,则这个正六边形的边长是 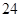
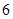

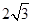




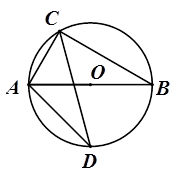



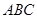 中,
中,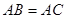 ,以
,以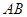 为直径的⊙O分别交
为直径的⊙O分别交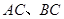 于点
于点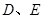 , 点
, 点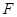 在
在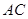 的延长线上,且
的延长线上,且 ∠
∠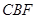
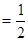 ∠
∠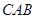 。
。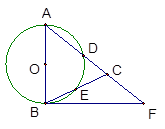
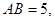 sin∠CBF=
sin∠CBF=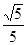 , 求BC和BF的长。
, 求BC和BF的长。 
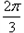 。
。




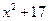 )
)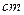 ,正六边形的边长为(
,正六边形的边长为( )cm(其中
)cm(其中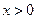 ),求这两段铁丝的总长
),求这两段铁丝的总长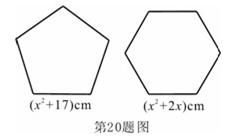

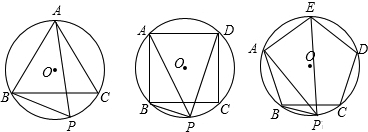
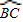 上一点,则PB+PC=PA;
上一点,则PB+PC=PA;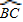 上一点,则
上一点,则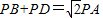 ;
; 上一点,请问PB+PE与PA有怎样的数量关系,写出结论,并加以证明;
上一点,请问PB+PE与PA有怎样的数量关系,写出结论,并加以证明; 上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.
上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明. 
 ∠AOB,∴AB=2BC.
∠AOB,∴AB=2BC. •
•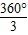 =60°,OC=r,
=60°,OC=r, •r•2r•tan60°=r2tan60°,
•r•2r•tan60°=r2tan60°,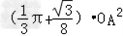 .
.
