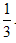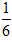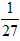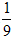二、 填空题 (共 15 小题)
收 起
把8个完全一样的小正方体拼成大正方体，表面积减少96平方厘米，原来每个小正方体的体积为( )。
一个长方体，如果高增加2厘米就成了正方体，并且表面积增加56平方厘米。原来这个长方体的体积是( )立方厘米。
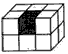
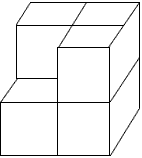
如下图，把一个棱长4厘米的正方体木块漆上红漆，再将它切成棱长1厘米的小正方体，这些小正方体中，只有1个面是红色的有( )块，有3个面是红色的有( )块，6个面全没涂漆的有( )块。
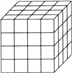
一个长方体，表面全部涂成红色后，被分割成若干个体积都等于1立方厘米的小正方体，如果在这些小正方体中，不带红色的小正方体的个数是8，两面带红色的小正方体的个数至多为( )。
一个正方体纸箱的表面积是24平方米，它的底面积是( )平方米。
把表面积是8平方米的正方体切成体积相等的8个小正方体，每个小正方体的表面积是( )。
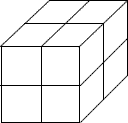
至少要( )个同样的小正方体才能拼出一个大正方体；如果一个小正方体的棱长是5厘米，那么大正方体的表面积是( )平方厘米，体积是( )立方厘米。
正方体棱长的总和是48厘米，它的表面积是( )平方厘米，体积是( )立方厘米。
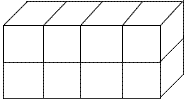
把下面的长方体和正方体粘合在一起，表面积减少了( )平方分米。
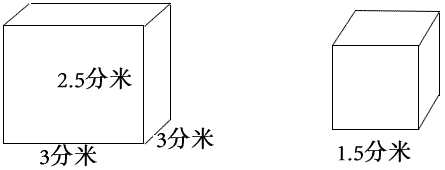
下图，把棱长为1dm的小正方体木块放在墙角，露在外面的面积是( )。
把一个长18厘米、宽14厘米、高10厘米的长方体，每次截下一个尽可能大的正方体，那么第三次截下的正方体的棱长是( )厘米。
一个正方体的棱长之和是24分米，则它的表面积是( )平方分米，体积是( )立方分米。
小明家有一个长方体的鱼缸，鱼缸的底是长为100厘米，宽为40厘米的长方形，里面放置一块棱长为10厘米的正方体石块，向鱼缸里加水，使水面没过石块，如果将石块取出，那么水面降低( )厘米。
把一个棱长是6厘米的正方体加工成一个最大的圆柱，这个圆柱的体积是( )，削去部分的体积是( )。
把一个棱长是6分米的正方体削成一个最大的圆锥，削去部分的体积是( )立方分米。
三、 应用题 (共 8 小题)
收 起
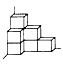
如下图，由三个正方体木块黏合而成的模型，它们的棱长分别是2分米，4分米和8分米。这个模型的表面积是多少？
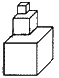
晚上放学回家，小强爸爸知道小强已经学习完了《圆柱和圆锥》这部分知识，于是，他出了个题目来检测小强。小强思考了一会就做出来了，相信你也会很快做出来。
题目：正方体内有一个最大的圆柱，圆柱的侧面积是25.12平方分米，这个正方体的表面积是多少平方分米？
下图表示一个正方体，它的棱长为4厘米，在它的上下、前后、左右的正中位置各挖去一个棱长为1厘米的正方体。问：此图的表面积是多少？
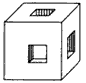
赵老师家有一个正方体木块，表面积是96cm2，把它锯成体积相等的8个正方体木块，每个小木块的表面积是多少？
一个正方体的棱长总和是72厘米，它的表面积是多少平方厘米？
一个长方体和一个正方体的棱长总和相等，已知长方体的长为10分米，宽为5分米，高为3分米，那么，正方体的棱长是多少分米？正方体的表面积是多少平方分米？正方体的体积是多少立方分米？
画一画，拼一拼，算一算
①在直径为6厘米的圆里剪去一个最大的正方形，求剩余面积
②一只蚂蚁沿着右图的边线绕了一圈，这只蚂蚁爬行了多少米？(图中单位：m)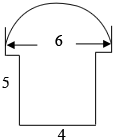
( ) 
( ) 
( ) 
( ) 
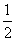
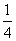
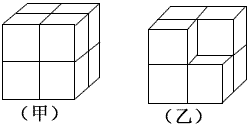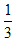，那么它的体积缩小到原来的( ) 
