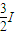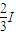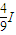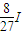

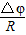 =
=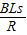 求解.指出该同学解法的错误之处,并用正确的方法解出结果.
求解.指出该同学解法的错误之处,并用正确的方法解出结果.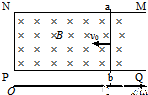

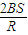
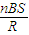
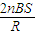
 ,再给它两端加上电压U,则( )
,再给它两端加上电压U,则( ) 
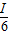

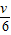
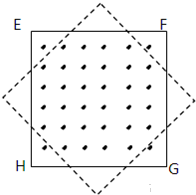
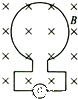
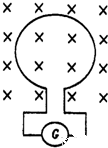 物理实验中,常用一种叫做“冲击电流计”的仪器测定通过电路的电量.如图所示,探测线圈与冲击电流计串联后可用来测定磁场的磁感应强度.已知线圈的匝数为n,面积为S,线圈与冲击电流计组成的回路电阻为R.若将线圈放在被测匀强磁场中,开始线圈平面与磁场垂直,现把探测圈翻转180°,冲击电流计测出通过线圈的电量为q,由上述数据可测出被测磁场的磁感应强度为( )
物理实验中,常用一种叫做“冲击电流计”的仪器测定通过电路的电量.如图所示,探测线圈与冲击电流计串联后可用来测定磁场的磁感应强度.已知线圈的匝数为n,面积为S,线圈与冲击电流计组成的回路电阻为R.若将线圈放在被测匀强磁场中,开始线圈平面与磁场垂直,现把探测圈翻转180°,冲击电流计测出通过线圈的电量为q,由上述数据可测出被测磁场的磁感应强度为( ) 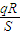
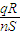

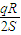
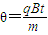
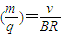
 如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两个过程中( )
如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两个过程中( ) 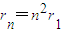 (n=1,2,3,…),其中n叫量子数.设氢原子的核外电子绕核近似做匀速圆周运动形成的等效电流,在n=2状态时其强度为I,则在n=3状态时等效电流强度为( )
(n=1,2,3,…),其中n叫量子数.设氢原子的核外电子绕核近似做匀速圆周运动形成的等效电流,在n=2状态时其强度为I,则在n=3状态时等效电流强度为( )