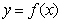 满足:
满足: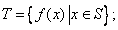 (ii)对任意
(ii)对任意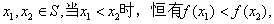
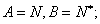
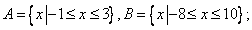
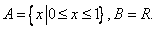
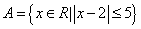 中最小整数位 .
中最小整数位 . 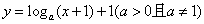 的图象必经过定点(0,1);
的图象必经过定点(0,1); :
: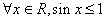 ,则
,则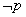 :
: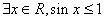 ;
;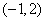 且与直线
且与直线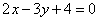 垂直的直线方程为
垂直的直线方程为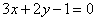 ;
;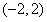 上随机抽取一个数
上随机抽取一个数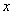 ,则
,则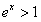 的概率为
的概率为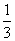 。
。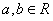 ,集合
,集合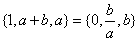 ,则
,则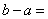 .
. 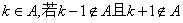 ,则k是A的一个“孤立元”,给定
,则k是A的一个“孤立元”,给定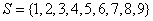 ,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。
,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。 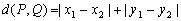 为两点
为两点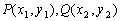 之间的“折线距离”,在这个定义下,给出下列命题:
之间的“折线距离”,在这个定义下,给出下列命题: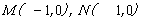 两点的“折线距离”之和为4的点的集合是面积为6的六边形;
两点的“折线距离”之和为4的点的集合是面积为6的六边形;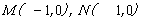 两点的“折线距离”差的绝对值为1的点的集合是两条平行线;
两点的“折线距离”差的绝对值为1的点的集合是两条平行线;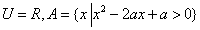 ,如果
,如果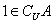 ,那么
,那么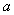 的取值范围是_____.
的取值范围是_____.