 用列举法可表示为 .
用列举法可表示为 . 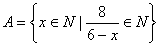 ,则用列举法表示集合
,则用列举法表示集合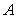 =______________ .
=______________ . 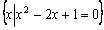 = ;
= ; 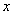 的不等式
的不等式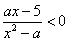 的解集是
的解集是 ,若
,若 ,则实数
,则实数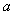 的取值范围是 .
的取值范围是 . 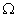 ,如果连接
,如果连接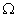 中任意两点的线段必定包含于
中任意两点的线段必定包含于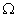 ,则称
,则称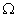 为平面上的凸集。给出平面上4个点集的图形如下(阴影区域及其边界):其中为凸集
为平面上的凸集。给出平面上4个点集的图形如下(阴影区域及其边界):其中为凸集
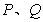 满足
满足 (其中
(其中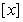 表示不超过
表示不超过 的最大整数,
的最大整数,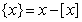 ),
), ,设
,设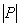 ,
,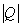 分别为集合
分别为集合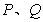 的元素个数,则
的元素个数,则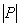 ,
,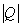 的大小关系为 .
的大小关系为 . 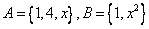 且
且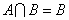 ,则
,则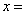 .
.  中只有一个元素,则
中只有一个元素,则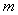 的值为________ .
的值为________ . 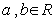 ,都有
,都有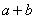 、
、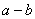 、
、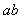 、
、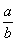 ∈P(除数b≠0),则称P是一个数域.例如有理数集Q是数域;数集
∈P(除数b≠0),则称P是一个数域.例如有理数集Q是数域;数集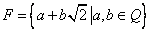 也是数域.有下列命题:①整数集是数域; ②若有理数集
也是数域.有下列命题:①整数集是数域; ②若有理数集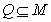 ,则数集M必为数域;③数域必为无限集; ④存在无穷多个数域.
,则数集M必为数域;③数域必为无限集; ④存在无穷多个数域.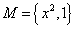 ,则实数
,则实数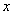 的取值范围为 .
的取值范围为 .